Diffraction par 1, 2 et N trous
circulaires
On considère un diaphragme circulaire de diamètre d
situé dans le plan z=0. Ce trou est éclaire par une
onde plane monochromatique de longueur d'onde 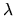 et d'amplitude
et d'amplitude 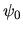 dans le plan du diaphragme. On s'intéresse à la figure de
diffraction à l'infini produite par ce trou. On notera
dans le plan du diaphragme. On s'intéresse à la figure de
diffraction à l'infini produite par ce trou. On notera 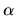 et
et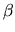 les deux premières coordonnées d'un vecteur unitaire définissant
une direction dans le demi-espace z>0.
les deux premières coordonnées d'un vecteur unitaire définissant
une direction dans le demi-espace z>0.
-
1.
-
Ecrire l'amplitude diffractée par le trou dans la direction (
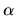 ,
,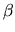 ).
Expliciter la transformée de Fourier sous forme d'une intégrale
et faire un passage en coordonnées polaires
).
Expliciter la transformée de Fourier sous forme d'une intégrale
et faire un passage en coordonnées polaires 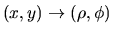 et
et 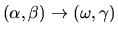 .
Introduire la fonction de Bessel J0 définie par
l'intégrale :
.
Introduire la fonction de Bessel J0 définie par
l'intégrale :
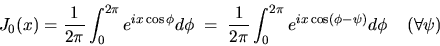
-
2.
-
Utiliser la relation
![$x\; J_0(x)=\frac{d}{dx}[x \; J_1(x)]$](img21.gif) (J1 est la fonction de Bessel du premier ordre) pour
exprimer l'amplitude diffractée dans la direction (
(J1 est la fonction de Bessel du premier ordre) pour
exprimer l'amplitude diffractée dans la direction (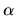 ,
,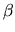 ).
Exprimer
).
Exprimer 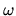 en fonction de l'angle
en fonction de l'angle 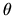 des coordonnées sphériques d'axe Oz. Montrer que la
figure obtenue est à symétrie de révolution.
des coordonnées sphériques d'axe Oz. Montrer que la
figure obtenue est à symétrie de révolution.
-
3.
-
Donner l'intensité
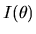 observée dans une direction d'angle
observée dans une direction d'angle 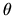 .
L'écrire en fonction de
.
L'écrire en fonction de 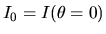 .
En vous aidant du graphe de la fonction d'Airy
.
En vous aidant du graphe de la fonction d'Airy ![${\cal A}(x)=[2\; J_1(x)/x]^2$](img26.gif) ,
dessiner l'allure de l'intensité qu'on observerait sur un écran
placé à une distance z assez grande pour que l'approximation
de Fraunhöffer soit vérifiée.
,
dessiner l'allure de l'intensité qu'on observerait sur un écran
placé à une distance z assez grande pour que l'approximation
de Fraunhöffer soit vérifiée.
Graphe de la fonction d'Airy ![$\left[2\; \frac{J_1(x)}{x}\right]^2$](img27.gif)
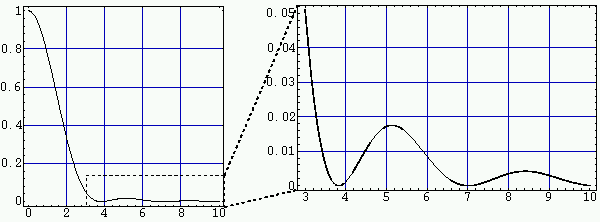
-
4.
-
Calculer le rayon angulaire et l'amplitude du premier anneau blanc
et des deux premiers anneaux noirs de l'intensité diffractée.
Le rayon angulaire est le demi-angle que sous-tend l'anneau vu depuis le
point O centre du diaphragme.
-
5.
-
On place maintenant dans le plan z=0 un masque constitué
de deux trous identiques de diamètre d séparés
d'une distance D. Ecrire le coefficient de transmission de l'ensemble,
calculer l'intensité diffractée dans une direction
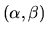 .
La figure obtenue est-elle encore à symétrie de révolution
? Combien y-a-t'il de franges dans la tache centrale à l'intérieur
du premier anneau noir ? Montrer que quand
.
La figure obtenue est-elle encore à symétrie de révolution
? Combien y-a-t'il de franges dans la tache centrale à l'intérieur
du premier anneau noir ? Montrer que quand 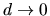 on retrouve les résultats connus sur les trous d'young.
on retrouve les résultats connus sur les trous d'young.
-
6.
-
On réalise un masque percé d'un grand nombre
 de trous de diamètre d. On pourra faire l'approximation
de trous de diamètre d. On pourra faire l'approximation 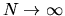 .
La position des trous sur le masque est aléatoire. Montrer que la
figure de diffraction à l'infini (intensité) est la même
que celle produite par un seul trou, mais N fois plus lumineuse.
Comment est modifiée la figure de diffraction si les trous, au lieu
d'être répartis aléatoirement, sont disposés
selon un réseau régulier carré de côté
a ?
.
La position des trous sur le masque est aléatoire. Montrer que la
figure de diffraction à l'infini (intensité) est la même
que celle produite par un seul trou, mais N fois plus lumineuse.
Comment est modifiée la figure de diffraction si les trous, au lieu
d'être répartis aléatoirement, sont disposés
selon un réseau régulier carré de côté
a ?
![]() et d'amplitude
et d'amplitude ![]() dans le plan du diaphragme. On s'intéresse à la figure de
diffraction à l'infini produite par ce trou. On notera
dans le plan du diaphragme. On s'intéresse à la figure de
diffraction à l'infini produite par ce trou. On notera ![]() et
et![]() les deux premières coordonnées d'un vecteur unitaire définissant
une direction dans le demi-espace z>0.
les deux premières coordonnées d'un vecteur unitaire définissant
une direction dans le demi-espace z>0.
![$\left[2\; \frac{J_1(x)}{x}\right]^2$](img27.gif)
