![]()
Calculer l'intensité diffractée à l'infini par un écran de coefficient de transmission décrit en coordonnées polaires par la distribution
![]()
avec ![]() et
et ![]() .
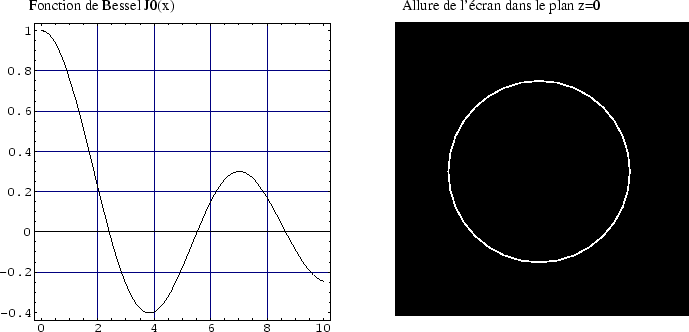
Cet écran modélise une couronne circulaire très fine
de rayon
.
Cet écran modélise une couronne circulaire très fine
de rayon ![]() (voir figure ci-après). On rappelle l'expression de la fonction
de Bessel
(voir figure ci-après). On rappelle l'expression de la fonction
de Bessel
A l'aide du graphe de la fonction ![]() ,
donner le rayon angulaire du premier anneau noir et du premier anneau brillant
de la figure de diffraction. Calculer le rapport entre l'intensité
au maximum du premier anneau brillant et l'intensité au centre de
la figure.
,
donner le rayon angulaire du premier anneau noir et du premier anneau brillant
de la figure de diffraction. Calculer le rapport entre l'intensité
au maximum du premier anneau brillant et l'intensité au centre de
la figure.