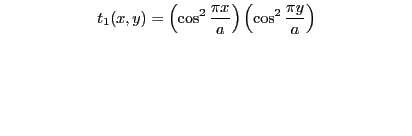

On considère une mire de coefficient de transmission
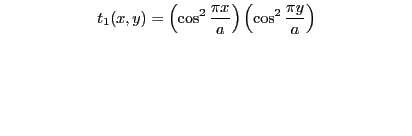

limitée par un diaphragme circulaire de rayon ![]() et éclairée sous incidence normale par une onde plane de longueur d'onde
et éclairée sous incidence normale par une onde plane de longueur d'onde ![]() et d'amplitude
et d'amplitude ![]() dans le plan de la mire pris comme origine des
dans le plan de la mire pris comme origine des ![]() . On observe la figure de diffraction à l'infini en un point de coordonnées
. On observe la figure de diffraction à l'infini en un point de coordonnées ![]() dans le plan
dans le plan ![]() avec
avec ![]() .
.