Filtrage en lumière
cohérente
On considère une mire de coefficient de transmission (en amplitude)

limitée par un diaphragme circulaire de
rayon 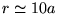 , son aspect est
celui de l'image ci-dessous.
, son aspect est
celui de l'image ci-dessous.

et éclairée sous incidence normale par une onde plane de
longueur d'onde 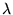 .
Cette mire est placée dans le plan P0 d'un montage
à double diffraction du type de celui de l'exercice suivant.
.
Cette mire est placée dans le plan P0 d'un montage
à double diffraction du type de celui de l'exercice suivant.
-
1.
-
Calculer l'intensité observée dans le plan P1.
Décrire la figure observée. A.N. :
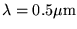 ,
, 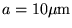 ,
f=1
m.
,
f=1
m.
-
2.
-
Dans le plan P1 on place une fente à 45
 de largeur 1 cm. Quelle est l'intensité dans le plan P2
? Décrire la figure observée, déterminer sa période
spatiale.
de largeur 1 cm. Quelle est l'intensité dans le plan P2
? Décrire la figure observée, déterminer sa période
spatiale.
-
3.
-
En plus de la fente, on place dans le plan P1 un petit
obstacle qui occulte l'ordre zéro. Quelle est l'intensité
dans le plan P2 ? Déterminer la période
spatiale de la nouvelle figure.
-
![]() , son aspect est
celui de l'image ci-dessous.
, son aspect est
celui de l'image ci-dessous.
