Strioscopie et contraste de phase

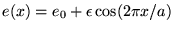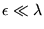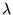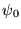On considère une lame de verre d'épaisseur légèrement variable et périodique $e(x)=e_0+\epsilon \cos(2\pi x/a)$ avec $\epsilon\ll \lambda$,$\lambda$ étant la longueur d'onde de l'onde incidente qui éclaire cette lame sous incidence normale. On appelle $\psi_0$ l'amplitude de cette onde dans le plan de la lame.

1.
Ecrire le coefficient de transmission t(x) de ce réseau. En faisant un développement limité, montrer qu'à la sortie de la lame on observe 3 ondes planes correspondant aux ordres 0 et 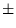$\pm$1.
2.
La lame est placée au foyer objet (plan P0) d'une lentille de focale f et de dimensions transversales infinies. Quelle est l'amplitude au foyer image (plan P1) ?

3.
On place une seconde lentille de focale f et dont le foyer objet se trouve dans le plan P1. On a ainsi réalisé un montage à double diffraction. Montrer que l'amplitude dans le plan image P2 de la deuxième lentille est proportionnelle à t1(-x). Quelle est l'intensité dans le plan P2 ?


4.
Technique de strioscopie : on place dans le plan P1, sur l'axe optique, on petit obstacle qui bloque l'ordre zéro. Ecrire l'intensité dans le plan P2. Montrer qu'elle est périodique et donner ses fréquences spatiales. Calculer le contraste de la figure.

5.
Technique de contraste de phase (Zernike, 1935) : on place cette fois dans le plan P1, sur l'axe optique, une petite lame parfaitement transparente qui déphase l'ordre zéro de $\pi/2$. Ecrire l'intensité dans le plan P2, montrer qu'elle est une fonction linéaire de la variation d'épaisseur t(x) de la lame. Quel est, à votre avis, l'intérêt de cette technique par rapport à la précédente (strioscopie) ? Calculer le contraste de la figure. 

6.
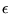L'oeil permet d'apprécier des contrastes supérieurs ou égaux à 5%. Calculer, pour les deux techniques, la valeur $\epsilon$ correspondante. Quelle est la technique qui vous semble la plus performante pour déceler des défauts d'épaisseur faibles sur des surfaces optiques ?