Défocalisation


 

On considère un objet éclairé par une onde monochromatique sous incidence normale de longueur d'onde 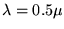$\lambda=0.5 \mu$m. Le coefficient de transmission, indépendant de y, s'écrit :

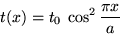
\begin{displaymath}t(x)=t_0 \: \cos^2 \frac{\pi x}{a}\end{displaymath}


Cet objet est situé dans le plan P0 du montage 3f ci-dessous. Le plan fccal de la première lentille P1 coincide avec la plan de la deuxième lentille. Les deux lentilles sont identiques, de focales f et de dimensions transversales infinies. On va étudier l'effet sur l'image d'une défocalisation, c'est à dire du cas où le plan d'observation P'2 ne coincide pas exactement avec le plan focal P2 de la deuxième lentille.

1.
On ne place rien dans le plan de filtrage. On note 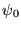$\psi_0$ l'amplitude de l'onde dans le plan de l'objet. Ecrire l'amplitude dans le plan P2.

2.
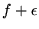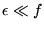La distance entre la deuxième lentille et le plan P'2 est $f+\epsilon$ avec $\epsilon \ll f$. Ecrire la diffraction de Fresnel entre la sortie de la deuxième lentille et le plan P'2. Montrer que l'image défocalisée (observée dans le plan P'2) est identique à l'image qui serait produite dans le plan focal P2 si on placait dans le plan de filtrage P1 une lentille l'(x,y) de convergence C faible que l'on précisera.

3.
On place dans le plan P1 une fente de largeur l. On n'introduit pas de défocalisation pour l'instant. Ecrire la fonction pupille dans le plan P1 et calculer la fonction de transfert de la propagation entre les plans P0 et P2. Quelle doit être la valeur de l pour que l'image observée soit uniforme ?

4.
On enlève la fente dans le plan P1 et on observe l'image défocalisée de t(x). On supposera que l'on observe dans le plan focal P2 et l'on simulera la défocalisation par la lentille l'(x,y). Ecrire la fonction pupille, calculer la fonction de transfert de la propagation.

5.
Calculer l'intensité dans le plan d'observation et décrire l'aspect de l'image. Quel est le contraste de la figure ? On défocalise progressivement en augmentant la valeur de C à partir de C=0. Quand l'intensité de l'objet filtré devient-elle uniforme pour la première fois ? Expliquer pourquoi, quand on continue à défocaliser, on obtient un objet filtré qui est à nouveau périodique mais dont les maxima d'intensité sont situés à la place des minima d'intensité de l'objet, puis un objet filtré uniforme, puis...etc.

6.
On remplace l'objet t(x) par la mire ci-dessous dont le coefficient de transmission s'écrit en première approximation 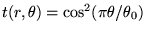$t(r,\theta)=\cos^2(\pi \theta/\theta_0)$ en coordonnées polaires. On étudie l'image défocalisée de cette mire.

(a)
Donner l'expression de la fréquence spatiale locale de cette mire en fonction de la distance au centre r.

(b)
La fonction 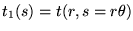$t_1(s)=t(r,s =r \theta)$ décrit les valeurs du coefficient de transmission sur un cercle de rayon r en fonction de l'abcisse curviligne s. En remarquant que cette fonction s'identifie à la mire sinusoïdale du début du problème, calculer le contraste à une distance r du centre de l'image de la mire.

(c)
Décrire l'aspect de l'image de la mire. Montrer que pour certaines régions on observe une inversion du contraste.