Diffraction de Fresnel : conservation
de l'énergie
Soit 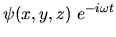 une onde monochromatique. Le point origine du système de coordonnées
est noté O. On note
une onde monochromatique. Le point origine du système de coordonnées
est noté O. On note 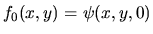 son amplitude complexe dans le plan z=0 et
son amplitude complexe dans le plan z=0 et 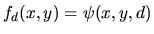 l'amplitude dans un plan de cote z=d. On se place dans l'approximation
de l'optique paraxiale.
l'amplitude dans un plan de cote z=d. On se place dans l'approximation
de l'optique paraxiale.
-
1.
-
Ecrire la transformée de Fresnel entre f0 et fd
sous la forme d'un produit de convolution. Expliciter la relation entre
les transformées de Fourier
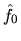 et
et 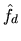
-
2.
-
Ecrire sous forme d'une intégrale l'énergie qui traverse
le plan z=0 en fonction de |f0|2
-
3.
-
Utiliser le théorème de Parseval pour montrer que l'énergie
qui traverse par unité de temps les plans z=0 et z=d
est la même. On rappelle que :
![\begin{displaymath}{\cal F}_{[u,v]} \left\{\frac{1}{i a}\; \exp \left(i\pi \frac......a}\right) \right\}\; = \; \exp \left(-i\pi a (u^2+v^2)\right)\end{displaymath}](img6.gif)
![]() une onde monochromatique. Le point origine du système de coordonnées
est noté O. On note
une onde monochromatique. Le point origine du système de coordonnées
est noté O. On note ![]() son amplitude complexe dans le plan z=0 et
son amplitude complexe dans le plan z=0 et ![]() l'amplitude dans un plan de cote z=d. On se place dans l'approximation
de l'optique paraxiale.
l'amplitude dans un plan de cote z=d. On se place dans l'approximation
de l'optique paraxiale.
![\begin{displaymath}{\cal F}_{[u,v]} \left\{\frac{1}{i a}\; \exp \left(i\pi \frac......a}\right) \right\}\; = \; \exp \left(-i\pi a (u^2+v^2)\right)\end{displaymath}](img6.gif)