Diffraction de Fresnel par
une lentille convergente
On considère une lentille convergente de rayon de courbure R,
d'indice n et de focale F. Cette lentille est placée
dans le plan z=0 et est supposée infinie. On note t(x',y')
son coefficient de transmission
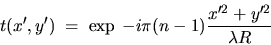
Cette lentille est éclairée par une onde plane monochromatique
sous incidence faible dont l'expression dans le plan z= 0 est :

On se place dans les conditions de l'optique paraxiale.
-
1.
-
Montrer que l'onde juste à la sortie de la lentille est sphérique.
On précisera les coordonnées (xs,ys,zs)
du centre de cette onde sphérique.
-
2.
-
Ecrire la transformée de Fourier-Fresnel pour obtenir l'amplitude
de l'onde dans un plan z quelconque. Montrer que l'onde obtenue
est également sphérique et préciser les coordonnées
de son centre.
-
3.
-
Montrer qu'il existe une valeur particulière de z pour laquelle
la lumière est totalement concentrée en un point. En déduire
la focale de cette lentille.
-
4.
-
On suppose que
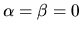 (incidence normale) et on se place sur l'axe optique (x=y=0).
Montrer que l'onde subit un déphasage de
(incidence normale) et on se place sur l'axe optique (x=y=0).
Montrer que l'onde subit un déphasage de 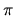 à la traversée du foyer.
à la traversée du foyer.