Diffraction de Fresnel par un bord d'écran

Un demi-plan (coefficient de transmission H(x)) placé dans le plan z=0 est éclairé sous incidence normale par une onde plane monochromatique de longueur d'onde $\lambda$. On cherche l'intensité diffractée à une distance z. On se place dans l'approximation de l'optique paraxiale.

1. Ecrire l'amplitude diffractée en un point de coordonnées (x, y, z>0) à l'aide de la fonction F(v)
 

$$F(v)=\int_{0}^v \exp i\pi \frac{t^2}{2} \; dt$$ (1)

appelée intégrale de Fresnel et dont la représentation dans le plan complexe est connue sous le nom de ``spirale de Cornu'' : les parties réelle X(v) et imaginaire Y(v) de cette fonction dessinent lorsque v varie la figure ci-dessous.
 



Faites un graphe de l'intensité (A.N. z=1 m, $\lambda=0.6 \; \mu$m), montrer qu'il existe des franges. Sont-elles équidistantes ?

2. L'occultation d'une étoile par la Lune peut se modéliser par une diffraction à distance finie par un bord d'écran. Le bord lunaire joue le rôle du demi-plan, éclairé par la lumière de l'étoile supposée à l'infini. La distance Terre-Lune étant de 400 000 km environ, donner la taille du premier interfrange (prendre $\lambda=0.5~\mu$m). La Lune tourne autour de la Terre en 28 jours environ et pour un observateur terrestre, elle se déplace par rapport aux étoiles. En combien de temps le train de franges balaie-t'il la France ? Donner l'allure du signal recueilli par un photomètre observant la disparition de l'étoile derrière le bord sombre de la lune (on graduera l'axe des temps en millisecondes).
3. Diffraction de Fresnel par une fente : écrire en fonction de F(v) l'amplitude diffractée en un point de coordonnées (x, y, z>0) par une fente de coefficient de transmission $\Pi(x/d)$ placée dans le plan z=0. Représenter le graphe de l'intensité lumineuse I(x,0) pour les valeurs z=32 cm et z=64 cm ($\lambda=0.5~\mu$m, d=1 mm).

Figure montrant l'évolution de l'intensité observée derrière un bord d'écran éclairé par une lumière laser de longueur d'onde 0.5 microns. Le noir correspond à l'absence de lumière. Le champ repréenté est un carré de 8 mm de côté. La distance entre le bord d'écran et l'observateur varie de 0 à (première image de la série) à 50 000 km pour la dernière image. La distance entre deux images est multipliée par un facteur 5 environ.

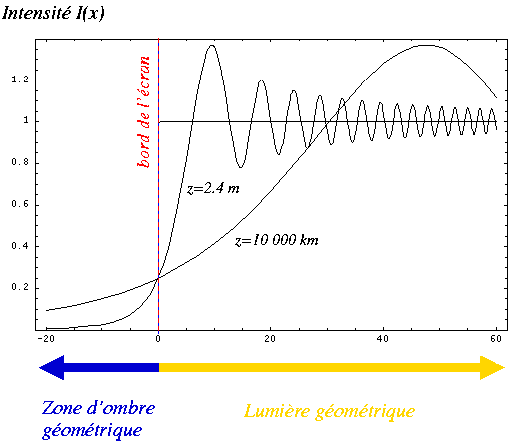
La figure ci-dessous montre le graphe de l'intensité en fonction de la distance transverse x (en dixièmes de mm) pour trois distances z entre l'écran et l'observateur. Remarquer les franges d'interférences dans la zône de droite correspondant à la partie qui serait uniformément éclairée s'il n'y avait pas de diffraction. On remarque aussi la présence d'un peu le lumière dans l'ombre géométrique de l'écran. Ce genre de figure est observé lors de la disparition d'une étoile derrière le bord lunaire. Les franges ont une taille de l'ordre de la dizaine de mètres à la surface de la Terre.