Fente fine de transmission en V

On considère une onde monochromatique de longueur d'onde 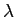$\lambda$ dont l'amplitude complexe s'écrit, dans le plan $z=0$ :

$$f_0(x,y)=A\, \delta(y)\, \vert x\vert\, \prod\left(\frac{x}{L}\right)$$

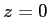avec 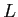$L$ un nombre réel positif. On se place dans les conditions de Gauss (approximation paraxiale).

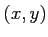1. Représenter schématiquement le graphe de $f_0(x,y)$ dans le plan $(x,y)$ (on supposera 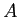$A$ réel positif)
2. Ecrire sous forme d'une intégrale l'expression de l'amplitude complexe en $(0,0,z)$
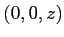
3. Faire le calcul de l'intégrale
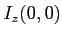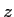4. En déduire l'intensité sur $I_z(0,0)$ sur l'axe et montrer qu'elle s'annule pour certaines valeurs de $z$.