Interférences et Fréquences
spatiales
Un écran percé de deux trous minuscules est placé
sur le trajet d'une onde électromagnétique plane de pulsation  et de vecteur d'onde
et de vecteur d'onde 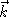 (
(  ). On rappelle qu'une telle onde s'écrit, en notation complexe,
). On rappelle qu'une telle onde s'écrit, en notation complexe, 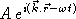 (ça ne sert à rien pour ce problème, c'est juste un
rappel). Les deux trous sont séparés d'un écart a.
On place à une distance d un écran d'observation E
comme sur le schéma ci-dessous.
(ça ne sert à rien pour ce problème, c'est juste un
rappel). Les deux trous sont séparés d'un écart a.
On place à une distance d un écran d'observation E
comme sur le schéma ci-dessous.
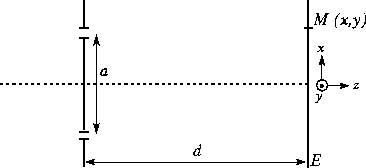
Chacun des deux trous se comporte comme une source secondaire émettant
une onde sphérique (on rappelle qu'une onde sphérique s'écrit
en un point M : 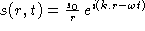 ,
, 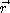 étant le vecteur qui joint la source de l'onde et le point M).
étant le vecteur qui joint la source de l'onde et le point M).
-
Calculer, en supposant
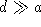 , l'intensité lumineuse I(x,y) des franges
d'interférences observées sur l'écran E (x
et y sont
, l'intensité lumineuse I(x,y) des franges
d'interférences observées sur l'écran E (x
et y sont 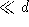 aussi).
aussi).
-
Ecrire le vecteur fréquence spatiale
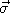 de cette figure d'interférences.
de cette figure d'interférences.
-
Un observateur se place à une distance D de l'écran
E. Quel est l'écart angulaire qu'il observe entre deux franges
brillantes successives ? En déduire les deux composantes
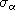 et
et 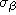 du vecteur fréquence angulaire
du vecteur fréquence angulaire 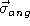 de la figure d'interférences. Donner la relation entre
de la figure d'interférences. Donner la relation entre 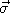 et
et 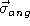 .
.
-
On fait tourner les deux trous d'un angle
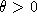 . Donner l'expression de la fréquence spatiale
. Donner l'expression de la fréquence spatiale 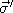 du nouveau système de franges I'(x,y). Donner
l'expression de I'(x,y).
du nouveau système de franges I'(x,y). Donner
l'expression de I'(x,y).
-
On s'intéresse à l'intersection de I'(x,y)
avec l'axe des x. Soit g(x) cette fonction. Montrer
que g(x) est périodique et calculer sa fréquence
spatiale
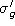 . Montrer que
. Montrer que 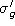 est la projection de
est la projection de 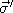 sur l'axe des x. Idem pour l'axe y. Montrer que cela ne marche
pas avec le ``vecteur période" T.
sur l'axe des x. Idem pour l'axe y. Montrer que cela ne marche
pas avec le ``vecteur période" T.
![]() et de vecteur d'onde
et de vecteur d'onde ![]() (
( ![]() ). On rappelle qu'une telle onde s'écrit, en notation complexe,
). On rappelle qu'une telle onde s'écrit, en notation complexe, ![]() (ça ne sert à rien pour ce problème, c'est juste un
rappel). Les deux trous sont séparés d'un écart a.
On place à une distance d un écran d'observation E
comme sur le schéma ci-dessous.
(ça ne sert à rien pour ce problème, c'est juste un
rappel). Les deux trous sont séparés d'un écart a.
On place à une distance d un écran d'observation E
comme sur le schéma ci-dessous.

![]() ,
, ![]() étant le vecteur qui joint la source de l'onde et le point M).
étant le vecteur qui joint la source de l'onde et le point M).