Identification d'une onde sphérique
On considère une onde sphérique monochromatique de longueur d'onde 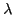 , se propageant dans le vide. Son amplitude complexe
, se propageant dans le vide. Son amplitude complexe 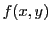 en un point
en un point 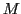 de coordonnées
de coordonnées 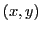 du plan
du plan 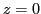 s'écrit, dans l'approximation paraxiale :
s'écrit, dans l'approximation paraxiale :
avec 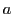 et
et 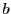 des constantes réelles positives, et
des constantes réelles positives, et 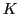 une constante complexe. On cherche à connaitre la position
une constante complexe. On cherche à connaitre la position 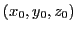 de la ``source''
de la ``source'' 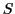 de l'onde.
de l'onde.
- Rappeler l'expression de l'amplitude complexe
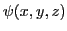 d'une onde sphérique monochromatique, convergente ou divergente, dont la source est située en
d'une onde sphérique monochromatique, convergente ou divergente, dont la source est située en 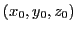
- Effectuer le développement limité habituel pour écrire
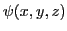 dans l'approximation paraxiale
dans l'approximation paraxiale
- Par identification avec
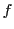 , préciser la position de la source
, préciser la position de la source 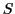 en fonction de
en fonction de 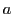 et
et 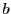 . Est-ce une onde sphérique convergente ou divergente ?
. Est-ce une onde sphérique convergente ou divergente ?