Superposition d'ondes planes

On considère une onde monochromatique non plane, de longueur d'onde 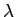$\lambda$, se propageant dans le vide. Son amplitude complexe 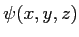$\psi(x,y,z)$ est connue dans le plan $z=0$ :

$$\psi(x,y,0)=\psi_0+\psi_1\: \sin\left(\frac{2\pi x}{a} \right)$$

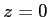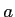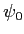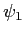avec $a$, $\psi_0$ et $\psi_1$ des constantes réelles positives. On suppose $\psi_1\ll \psi_0$.

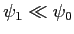1. Ecrire l'intensité 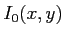$I_0(x,y)$ de l'onde dans le plan 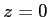$z=0$, tracez son graphe.
2. Montrer que l'onde est la somme de plusieurs ondes planes monochromatiques, préciser les vecteurs d'onde associés (pas d'approximation paraxiale pour l'instant)
3. En déduire l'amplitude complexe 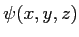$\psi(x,y,z)$ de l'onde quelle que soit la valeur de $z$.
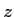4. Ecrire l'intensité 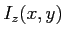$I_z(x,y)$ dans un plan 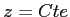$z=Cte$ quelconque
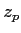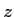5. Montrer qu'il existe des valeurs $z_p$ de $z$ pour lesquelles l'intensité est uniforme
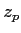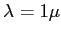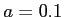6. Que vaut $z_p$ dans l'approximation paraxiale ? A.N. : $\lambda=1\mu$m, $a=0.1$ mm