Interféromètre
de Michelson
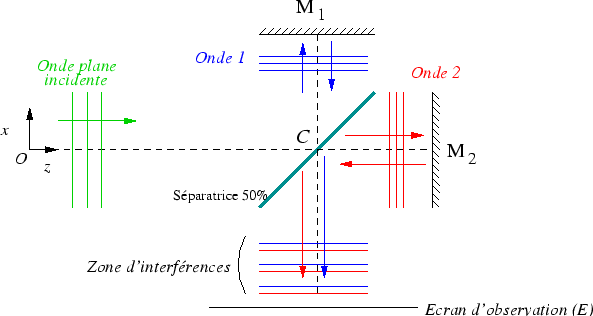
Un interféromètre de Michelson est éclairé par
une onde plane arrivant parallèlement à l'axe optique de l'interféromètre.
Les interférences sont observées dans le plan 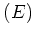 de la figure ci-après, au voisinage de l'axe optique.
On pose
de la figure ci-après, au voisinage de l'axe optique.
On pose 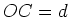 ,
, 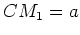 ,
, 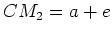 et
et 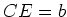 . Le décalage réglable
. Le décalage réglable
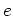 permet de réaliser une différence de marche entre
les deux ondes secondaires produites par la séparatrice (On dit
dans ce cas que l'interféromètre est réglé en
``teinte plate''). La lame séparatrice est supposée d'épaisseur
nulle et de coefficient de réflexion et de transmission en intensité
égaux à 0.5 (les deux ondes à la sortie ont une
intensité
moitié de celle de l'onde incidente). L'onde incidente,
supposée parfaitement cohérente est
issue d'un laser He-Ne délivrant une longueur d'onde
permet de réaliser une différence de marche entre
les deux ondes secondaires produites par la séparatrice (On dit
dans ce cas que l'interféromètre est réglé en
``teinte plate''). La lame séparatrice est supposée d'épaisseur
nulle et de coefficient de réflexion et de transmission en intensité
égaux à 0.5 (les deux ondes à la sortie ont une
intensité
moitié de celle de l'onde incidente). L'onde incidente,
supposée parfaitement cohérente est
issue d'un laser He-Ne délivrant une longueur d'onde 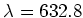 nm.
nm.
- On réalise
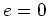 . Ecrire
l'intensité dans le plan E en fonction de e.
Décrire le phénomène observé quand on déplace le miroir
. Ecrire
l'intensité dans le plan E en fonction de e.
Décrire le phénomène observé quand on déplace le miroir 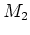 Quelle est la différence de marche
Quelle est la différence de marche 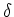 entre les deux
ondes ? Quelles sont les valeurs de
entre les deux
ondes ? Quelles sont les valeurs de 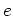 réalisant une
interférence constructive ? Destructive ?
réalisant une
interférence constructive ? Destructive ?
- Ecrire l'intensité
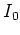 au centre de l'écran
au centre de l'écran 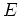 en fonction de la variable
en fonction de la variable 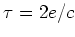 . Que représente
cette variable (on peut déterminer sa dimension) ? Tracer la
courbe
. Que représente
cette variable (on peut déterminer sa dimension) ? Tracer la
courbe 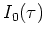 , déterminer sa période.
, déterminer sa période.
- On incline le miroir
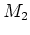 d'un angle
d'un angle 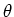 faible
autour de l'axe
faible
autour de l'axe 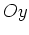 (On dit alors que l'interféromètre
est réglé en ``coin d'air'')
(On dit alors que l'interféromètre
est réglé en ``coin d'air'')
- Ecrire les vecteurs d'onde
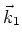 et
et 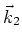 des deux ondes planes qui interfèrent sur l'écran
des deux ondes planes qui interfèrent sur l'écran
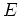 .
.
- Relier la position d'un point
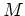 sur l'écran
sur l'écran
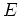 au déphasage entre les deux ondes, puis
à leur différence de marche
au déphasage entre les deux ondes, puis
à leur différence de marche 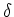 et au retard
et au retard  entre les deux ondes. Prédire
les points de
entre les deux ondes. Prédire
les points de 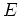 où l'on observera une frange brillante
et une frange sombre.
où l'on observera une frange brillante
et une frange sombre.
- Ecrire l'intensité lumineuse sur l'écran
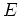 , décrire l'aspect du champ d'interférences, l'interfrange.
, décrire l'aspect du champ d'interférences, l'interfrange.
- On remplace l'onde plane incidente par une onde sphérique (même
longueur d'onde) issue d'une source ponctuelle se trouvant en
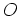 . Le michelson est réglé en teinte plate. On se
place dans l'approximation de Gauss (paraxiale).
. Le michelson est réglé en teinte plate. On se
place dans l'approximation de Gauss (paraxiale).
- On réalise
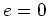 . Qu'observe-t'on dans le plan
. Qu'observe-t'on dans le plan 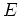 ?
?
- Ecrire l'intensité en
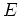 pour
pour 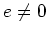 . Montrer l'existence d'anneaux d'interférence et
calculer l'interfrange (distance entre deux anneaux brillants successifs).
. Montrer l'existence d'anneaux d'interférence et
calculer l'interfrange (distance entre deux anneaux brillants successifs).

![]() de la figure ci-après, au voisinage de l'axe optique.
On pose
de la figure ci-après, au voisinage de l'axe optique.
On pose ![]() ,
, ![]() ,
, ![]() et
et ![]() . Le décalage réglable
. Le décalage réglable
![]() permet de réaliser une différence de marche entre
les deux ondes secondaires produites par la séparatrice (On dit
dans ce cas que l'interféromètre est réglé en
``teinte plate''). La lame séparatrice est supposée d'épaisseur
nulle et de coefficient de réflexion et de transmission en intensité
égaux à 0.5 (les deux ondes à la sortie ont une
intensité
moitié de celle de l'onde incidente). L'onde incidente,
supposée parfaitement cohérente est
issue d'un laser He-Ne délivrant une longueur d'onde
permet de réaliser une différence de marche entre
les deux ondes secondaires produites par la séparatrice (On dit
dans ce cas que l'interféromètre est réglé en
``teinte plate''). La lame séparatrice est supposée d'épaisseur
nulle et de coefficient de réflexion et de transmission en intensité
égaux à 0.5 (les deux ondes à la sortie ont une
intensité
moitié de celle de l'onde incidente). L'onde incidente,
supposée parfaitement cohérente est
issue d'un laser He-Ne délivrant une longueur d'onde ![]() nm.
nm. 