Diffraction de Fresnel derrière
un réseau sinusoïdal
Soit un réseau de coefficient de transmission
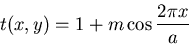
avec 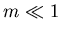 .
Ce réseau est éclairé par une onde plane de longueur
d'onde
.
Ce réseau est éclairé par une onde plane de longueur
d'onde 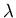 arrivant sous incidence normale. On note
arrivant sous incidence normale. On note  l'amplitude complexe incidente dans le plan du réseau pris comme
origine des
l'amplitude complexe incidente dans le plan du réseau pris comme
origine des 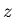 .
.
-
Ecrire l'amplitude complexe de l'onde émergente dans le plan du
réseau. La décomposer en somme discrète d'ondes planes.
Dans quelles directions de cosinus directeurs
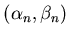 ces ondes se propagent-elles ?
ces ondes se propagent-elles ?
-
A quelle condition sur la période du réseau peut-on traiter
le problème en utilisant l'approximation de Gauss ? Dans la suite
on supposera cette condition réalisée.
-
Ecrire l'amplitude complexe dans un plan
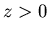 ,
puis l'intensité correspondante. Calculer le contraste
,
puis l'intensité correspondante. Calculer le contraste 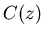 de l'intensité.
de l'intensité.
-
Montrer que l'intensité
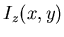 devient uniforme pour certaines valeurs de
devient uniforme pour certaines valeurs de 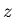 .
A.N.:
.
A.N.: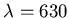 nm,
nm, 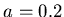 mm.
mm.
-
Montrer qu'il existe des valeurs de
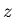 pour lesquelles l'intensité est identique à celle observée
dans le plan du réseau.
pour lesquelles l'intensité est identique à celle observée
dans le plan du réseau.
-
Montrer qu'il existe des valeurs de
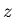 pour lesquelles l'intensité est identique à celle observée
dans le plan du réseau, mais avec une inversion des franges brillantes
et sombres
pour lesquelles l'intensité est identique à celle observée
dans le plan du réseau, mais avec une inversion des franges brillantes
et sombres
![]() .
Ce réseau est éclairé par une onde plane de longueur
d'onde
.
Ce réseau est éclairé par une onde plane de longueur
d'onde ![]() arrivant sous incidence normale. On note
arrivant sous incidence normale. On note ![]() l'amplitude complexe incidente dans le plan du réseau pris comme
origine des
l'amplitude complexe incidente dans le plan du réseau pris comme
origine des ![]() .
.