Cet instrument (lentille+masque) est complètement caractérisé par sa réponse impulsionnelle angulaire
![]() (l'image au foyer est la convolution de l'objet par la réponse impulsionnelle) ou sa fonction de transfert
(l'image au foyer est la convolution de l'objet par la réponse impulsionnelle) ou sa fonction de transfert
![]() .
Les deux fonctions font intervenir le coefficient de transmission du masque P(x,y), appelé fonction pupille de l'instrument.
.
Les deux fonctions font intervenir le coefficient de transmission du masque P(x,y), appelé fonction pupille de l'instrument.
Un instrument optique plus compliqué avec plusieurs lentilles, des diaphragmes, etc...peut aussi être caractérisé par une réponse impulsionnelle prenant en compte l'ensemble des éléments optiques. Un tel instrument possèdera généralement une pupille d'entrée et une pupille de sortie. Une définition naïve de la pupille d'entrée pourrait ètre le coefficient de transmission du premier dioptre traversé. L'exemple de la figure ci-dessous montre que c'est un en fait peu plus compliqué :
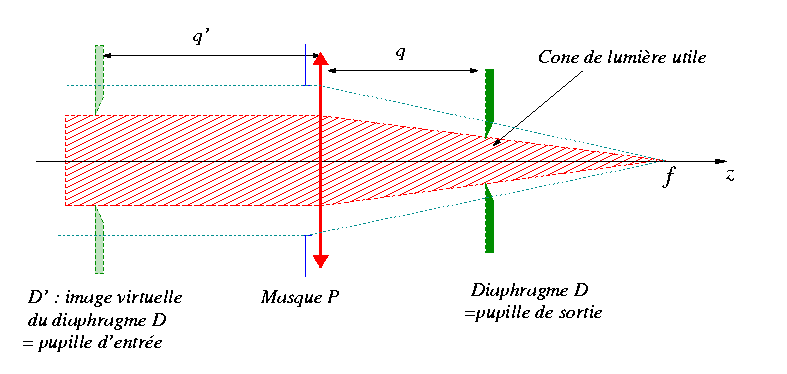
Le système optique est composé d'une lentille limistée spatialement par un masque P, et d'un petit diaphragme ![]() qui limite la zône utile du faisceau. Ce diaphragme est placé à une distance q de la lentille. Seule la lumière passant dans la partie grisée participe à la formation de l'image. Tout se passe comme si on avait un diaphragme
qui limite la zône utile du faisceau. Ce diaphragme est placé à une distance q de la lentille. Seule la lumière passant dans la partie grisée participe à la formation de l'image. Tout se passe comme si on avait un diaphragme ![]() ,
image virtuelle de
,
image virtuelle de ![]() située avant la lentille à une distance q' telle que
située avant la lentille à une distance q' telle que
![]() (formule de conjugaison). Dans ce cas
(formule de conjugaison). Dans ce cas ![]() est la pupille de sortie et
est la pupille de sortie et ![]() la pupille d'entrée.
la pupille d'entrée.
On peut adopter les définitions suivantes