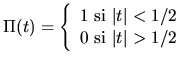
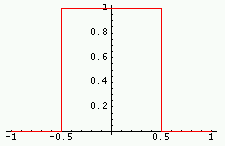
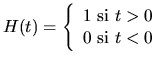
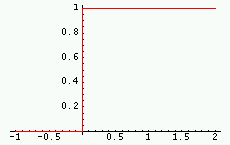
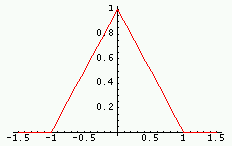
![$\displaystyle\Lambda(t)=\left\{\begin{array}{l}1 -\vert t] \mbox{ si } \vert t\vert\le 1 \\0 \mbox{ sinon }\end{array} \right.$](img5.gif)
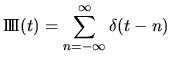
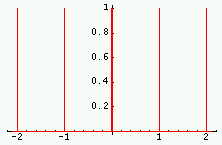
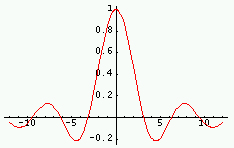
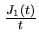
| Fonction | Transformée | Fonction | Transformée |
 |
|||
 |
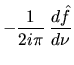 |
||
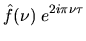 Animation (340 KB) |
|||
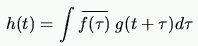 |
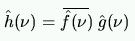 |
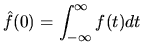 |
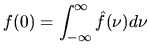 |
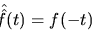 |
| Th. de Parseval | 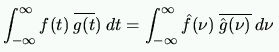 |
|
| (partie réelle paire, partie imaginaire impaire) |
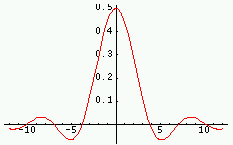
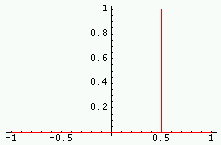
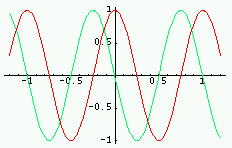
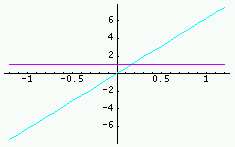
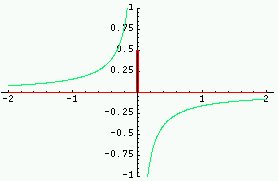
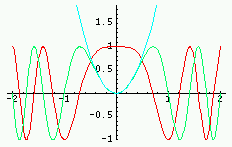
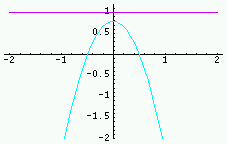
| Fonction | Graphe de la fonction Rouge : partie réelle ; Vert : imaginaire ; Violet : module ; Cyan : phase |
Transformée | Graphe de la TF (parties réelle/imag ; module/phase) |
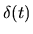 |
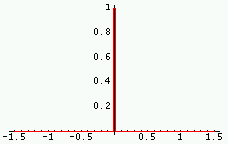 |
1 | 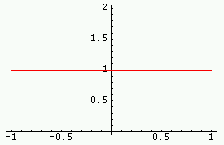 |
| 1 |  |
 |
|
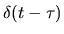 |
 |
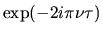 |
 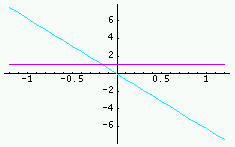 |
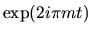 |
 |
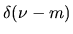 |
 |
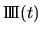 |
 |
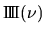 |
 |
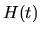 |
 |
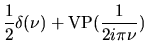 |
 |
 |
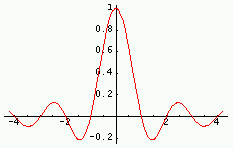 |
||
 |
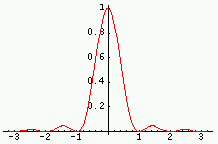 |
||
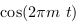 |
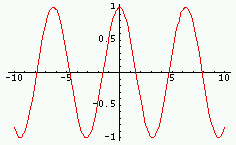 |
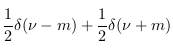 |
 |
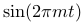 |
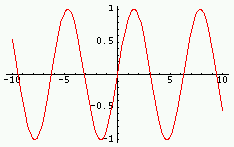 |
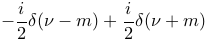 |
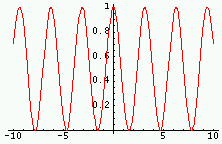
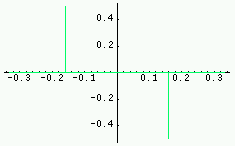 |
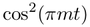 |
 |
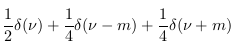 |
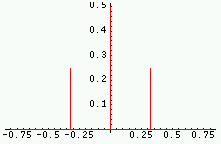 |
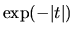 |
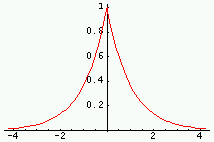 |
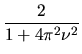 |
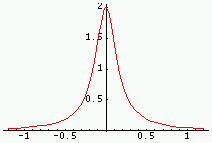 |
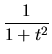 |
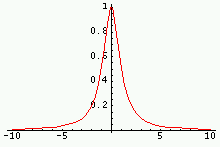 |
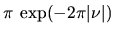 |
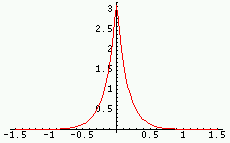 |
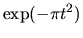 |
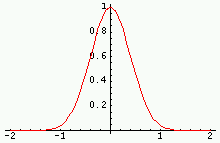 |
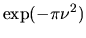 |
 |
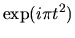 |
 |
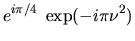 |
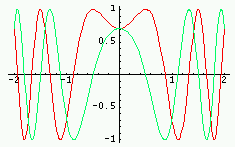  |
![]()
et
![]()
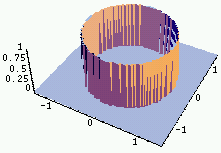
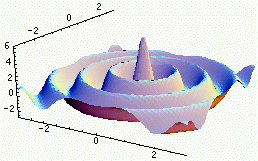
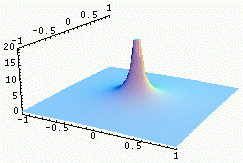
| Fonction | Graphe de la fonction | Transformée | Graphe de la TF |
 |
 |
||
 |
 |
||
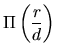 |
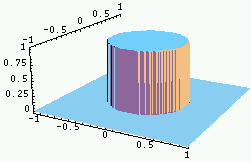 |
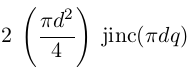 |
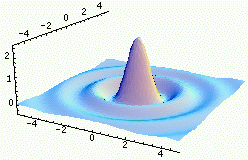 |
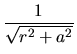 |
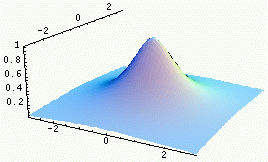 |
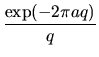 |
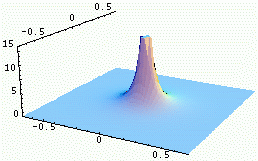 |
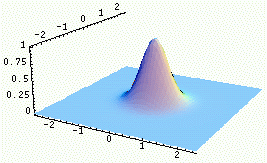 |
 |
||
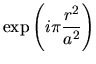 |
Partie réelle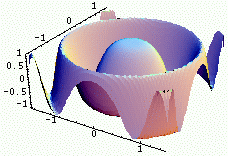 |
Partie réelle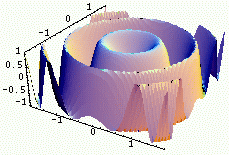 |
|
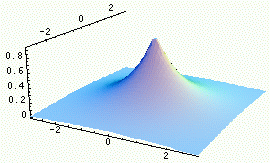 |
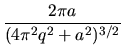 |
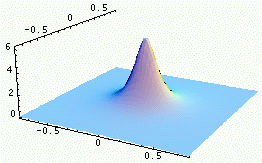 |
|