Licence de Physique LP2
Quatrième interrogation d'optique
Cours et TD autorisés
Interférences avec un spectre cannelé
Durée 30 mn
On réalise une expérience d'interférences en éclairant
un dispositif de trous d'Young avec une onde plane polychromatique arrivant
sous incidence normale. La distance entre les deux trous, alignés
le long de l'axe 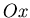 est
est 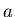 ,
les franges sont observées sur un écran
,
les franges sont observées sur un écran 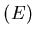 placé à une distance
placé à une distance 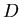 du plan des trous. On appelle
du plan des trous. On appelle 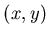 les coordonnées d'un point
les coordonnées d'un point 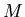 de
de 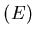 où l'on observe les franges d'interférences.
où l'on observe les franges d'interférences.
Le spectre de la lumière est de la forme
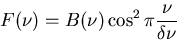
où 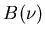 est le spectre de la lumière blanche, modélisé par
une gaussienne de largeur
est le spectre de la lumière blanche, modélisé par
une gaussienne de largeur  centrée sur la fréquence
centrée sur la fréquence  .
.
-
Dessiner grossièrement le spectre de l'onde incidente lorsque
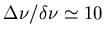 .
Pourquoi parle-t'on de spectre cannelé ? Quel est l'ordre de grandeur
du nombre de cannelures dans
.
Pourquoi parle-t'on de spectre cannelé ? Quel est l'ordre de grandeur
du nombre de cannelures dans 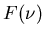 ?
?
-
Calculer le degré de cohérence temporelle de l'onde incidence.
-
Que représente la variable
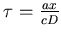 (
( =vitesse
de la lumière) ? Ecrire l'intensité moyenne des franges d'interférences
au point
=vitesse
de la lumière) ? Ecrire l'intensité moyenne des franges d'interférences
au point 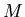 .
.
-
Dessiner l'aspect du champ d'interférences lorsque
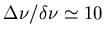 montrer qu'on observe dans ce cas trois paquets de franges centrées
en
montrer qu'on observe dans ce cas trois paquets de franges centrées
en 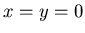 et
et 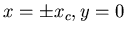 ,
calculer
,
calculer 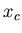 .
.
-
Combien observe-t'on de franges dans chaque paquet ? A.N : le spectre
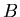 de la lumière blanche est centré sur la longueur 500 nm et
possède une demi-largeur de 200 nm. Quelle condition doit-on remplir
pour qu'il n'y ait pas de recouvrement entre les trois paquets ?
de la lumière blanche est centré sur la longueur 500 nm et
possède une demi-largeur de 200 nm. Quelle condition doit-on remplir
pour qu'il n'y ait pas de recouvrement entre les trois paquets ?
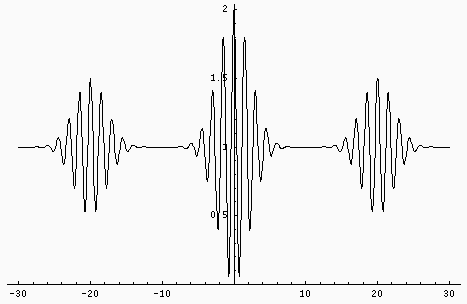
La figure ci-dessous montre l'aspect du champ d'interférences
avec un spectre cannelé :

![]() est
est ![]() ,
les franges sont observées sur un écran
,
les franges sont observées sur un écran ![]() placé à une distance
placé à une distance ![]() du plan des trous. On appelle
du plan des trous. On appelle ![]() les coordonnées d'un point
les coordonnées d'un point ![]() de
de ![]() où l'on observe les franges d'interférences.
où l'on observe les franges d'interférences.
![]() est le spectre de la lumière blanche, modélisé par
une gaussienne de largeur
est le spectre de la lumière blanche, modélisé par
une gaussienne de largeur ![]() centrée sur la fréquence
centrée sur la fréquence ![]() .
.

