Licence de Physique LP2
Troisième interrogation d'optique
Cours et TD autorisés
Formation d'images
Durée 30 mn
On considère une lentille mince convergente de focale 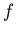 limitée spatialement par un diaphragme circulaire de diamètre
limitée spatialement par un diaphragme circulaire de diamètre 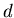 (une optique le longue-vue par exemple). Cette lentille, placée
dans le plan
(une optique le longue-vue par exemple). Cette lentille, placée
dans le plan 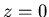 est éclairée en lumière monochromatique par un point
source
est éclairée en lumière monochromatique par un point
source 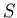 situé en un point de coordonnées
situé en un point de coordonnées 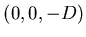 avec
avec 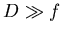 (suffisamment grand pour faire l'approximation de la diffraction de Fraunhoffer).
Le montage est le suivant :
(suffisamment grand pour faire l'approximation de la diffraction de Fraunhoffer).
Le montage est le suivant :
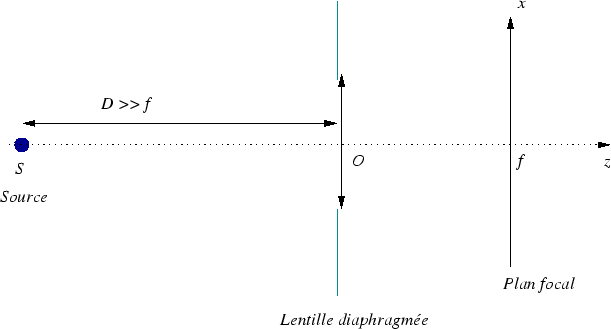
-
Ecrire l'amplitude à l'entrée de la lentille diaphragmée.
-
Ecrire l'amplitude dans le plan focal image, puis l'intensité, et
faire un schéma. (A.N.:
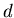 =1
cm,
=1
cm, 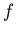 =10
cm,
=10
cm, 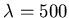 nm).
nm).
-
On déplace légèrement la source
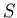 dans la direction
dans la direction 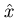 .
On appelle
.
On appelle 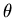 l'angle que fait la direction
l'angle que fait la direction 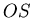 avec l'axe optique (
avec l'axe optique (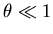 ).
Quelle est la nouvelle expression de l'intensité dans le plan focal
image de la lentille ?
).
Quelle est la nouvelle expression de l'intensité dans le plan focal
image de la lentille ?
-
On éclaire maintenant avec deux points sources identiques incohérents
entre eux, l'un situé sur l'axe optique, l'autre dans la direction
d'angle
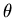 de la question précédente. Ecrire l'intensité dans
le plan focal image.
de la question précédente. Ecrire l'intensité dans
le plan focal image.
-
Proposez un calcul du pouvoir de résolution de la lentille diaphragmée
: angle
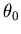 à partir duquel les deux points sources donnent deux images ``bien
séparées'' (inspirez-vous du raisonnement fait en cours
pour calculer le pouvoir de résolution des réseaux).
Quel diamètre doit avoir un télescope pour résoudre
un homme sur la Lune (distance Terre-Lune : 400 000 km) ?
à partir duquel les deux points sources donnent deux images ``bien
séparées'' (inspirez-vous du raisonnement fait en cours
pour calculer le pouvoir de résolution des réseaux).
Quel diamètre doit avoir un télescope pour résoudre
un homme sur la Lune (distance Terre-Lune : 400 000 km) ?
![]() limitée spatialement par un diaphragme circulaire de diamètre
limitée spatialement par un diaphragme circulaire de diamètre ![]() (une optique le longue-vue par exemple). Cette lentille, placée
dans le plan
(une optique le longue-vue par exemple). Cette lentille, placée
dans le plan ![]() est éclairée en lumière monochromatique par un point
source
est éclairée en lumière monochromatique par un point
source ![]() situé en un point de coordonnées
situé en un point de coordonnées ![]() avec
avec ![]() (suffisamment grand pour faire l'approximation de la diffraction de Fraunhoffer).
Le montage est le suivant :
(suffisamment grand pour faire l'approximation de la diffraction de Fraunhoffer).
Le montage est le suivant :
