Licence de Physique 2002-2003
Troisième interrogation d'optique
Cours et TD autorisés
Filtrage d'une mire sinusoïdale
Durée 30 mn
On possède une grille sinusoïdale 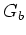 de coefficient
de transmission
de coefficient
de transmission 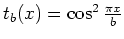 et de période
et de période 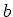 inconnue. On possède par ailleurs une autre mire sinusoïdale
inconnue. On possède par ailleurs une autre mire sinusoïdale
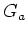 de coefficient de transmission
de coefficient de transmission
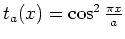 avec
avec 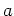 parfaitement connu,
de lentilles convergentes de de diverses focales, et d'un laser de longueur
d'onde
parfaitement connu,
de lentilles convergentes de de diverses focales, et d'un laser de longueur
d'onde 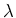 . On cherche à déterminer la
période inconnue
. On cherche à déterminer la
période inconnue 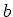 à partir d'une expérience
de filtrage optique. Le schéma est le montage
à partir d'une expérience
de filtrage optique. Le schéma est le montage 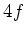 classique
de la figure ci-dessous :
classique
de la figure ci-dessous :
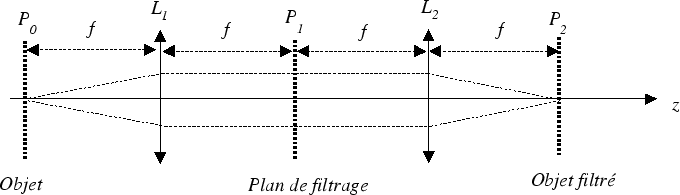
La grille 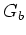 est placée dans le plan
est placée dans le plan 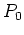 , au foyer objet de la lentille
, au foyer objet de la lentille 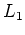 . L'éclairage
se fait sous incidence normale. La grille
. L'éclairage
se fait sous incidence normale. La grille 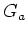 est placée
dans le plan
est placée
dans le plan 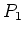 , au foyer image de la lentille
, au foyer image de la lentille 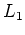 . Les deux lentilles sont de focale
. Les deux lentilles sont de focale 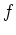 , le plan
focal objet de
, le plan
focal objet de 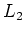 est confondu avec le plan focal image de
est confondu avec le plan focal image de 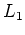 . On observe le résultat du filtrage dans le plan
. On observe le résultat du filtrage dans le plan 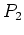 .
.
- Ecrire la réponse impulsionnelle du filtrage effectué.
- En déduire l'amplitude complexe dans le plan
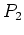 .
.
- Comment doit-on choisir la focale
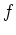 pour obtenir une image
uniforme dans le plan
pour obtenir une image
uniforme dans le plan 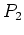 ? On rappelle que
? On rappelle que
- Proposez une autre expérience optique qui permettrait de déterminer
la valeur de
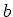 .
.


![]() est placée dans le plan
est placée dans le plan ![]() , au foyer objet de la lentille
, au foyer objet de la lentille ![]() . L'éclairage
se fait sous incidence normale. La grille
. L'éclairage
se fait sous incidence normale. La grille ![]() est placée
dans le plan
est placée
dans le plan ![]() , au foyer image de la lentille
, au foyer image de la lentille ![]() . Les deux lentilles sont de focale
. Les deux lentilles sont de focale ![]() , le plan
focal objet de
, le plan
focal objet de ![]() est confondu avec le plan focal image de
est confondu avec le plan focal image de ![]() . On observe le résultat du filtrage dans le plan
. On observe le résultat du filtrage dans le plan ![]() .
.