Licence de Physique 2002-2003
Quatrième interrogation d'optique
Cours et TD autorisés
Cohérence temporelle
Durée 30 mn
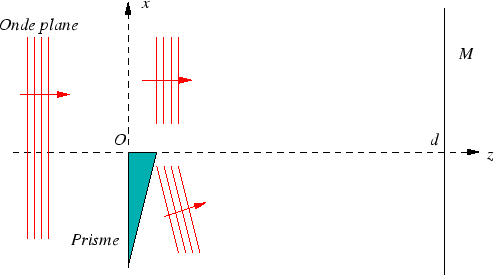
Une onde plane se propage le long des 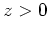 . Dans le plan
. Dans le plan 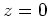 elle rencontre un prisme introduisant une déviation
faible
elle rencontre un prisme introduisant une déviation
faible 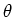 qui occupe le demi-plan
qui occupe le demi-plan 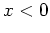 . Une partie
de la lumière est donc déviée et vient interférer
avec la partie qui n'est pas déviée. On s'intéresse
à l'intensité en un point
. Une partie
de la lumière est donc déviée et vient interférer
avec la partie qui n'est pas déviée. On s'intéresse
à l'intensité en un point 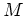 de coordonnées
de coordonnées
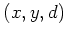 . On négligera les effets de diffraction dûs
aux bords du prisme.
. On négligera les effets de diffraction dûs
aux bords du prisme.
- L'éclairage est monochromatique, la longueur d'onde est
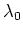 . L'amplitude de l'onde incidente dans le plan
. L'amplitude de l'onde incidente dans le plan 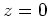 est
est 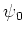 . Ecrire l'intensité au point
. Ecrire l'intensité au point 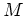 . Donner l'interfrange.
. Donner l'interfrange.
- L'onde incidente est maintenant constituée de la somme de deux
vibrations, le spectre étant de la forme
avec 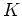 une constante,
une constante, 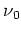 la fréquence
centrale et
la fréquence
centrale et 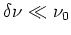 la différence des fréquences des
deux vivrations. Ecrire l'intensité au point
la différence des fréquences des
deux vivrations. Ecrire l'intensité au point 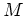 . On pourra
poser
. On pourra
poser 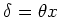 . Tracer
le graphe de l'intensité en fonction de
. Tracer
le graphe de l'intensité en fonction de  .
.
- Donner le contraste des franges en fonction de
 . Montrer
que le contraste s'inverse (changement de signe de la visibilité complexe)
pour certaines valeurs.
. Montrer
que le contraste s'inverse (changement de signe de la visibilité complexe)
pour certaines valeurs.
- Question qualitative : Comment serait modifiée la figure
d'interférences (intensité en
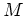 ) si le spectre de la
lumière n'était pas composé de deux Diracs, mais de
deux petites gaussiennes identiques de largeur
) si le spectre de la
lumière n'était pas composé de deux Diracs, mais de
deux petites gaussiennes identiques de largeur 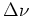 ?
Dessiner l'allure du champ d'interférences pour
?
Dessiner l'allure du champ d'interférences pour