Licence de Physique 2003-2004
Troisième interrogation d'optique
Cours et TD autorisés
Filtrage dérivateur
Durée 30 mn
Soit un écran de coefficient de transmission 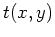 placé
dans le montage
placé
dans le montage 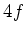 à double diffraction de la figure ci-dessous :
à double diffraction de la figure ci-dessous :
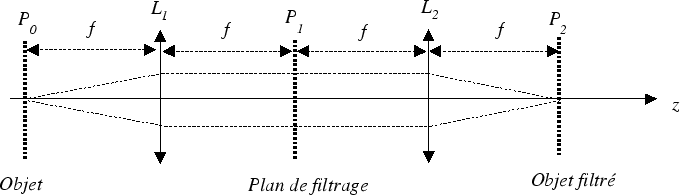
L'éclairage se fait par une onde plane sous incidence normale,
d'amplitude 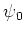 dans le plan
dans le plan 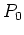 et de longueur d'onde
et de longueur d'onde
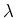 . Les deux lentilles sont de focale
. Les deux lentilles sont de focale 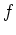 , le plan
focal objet de
, le plan
focal objet de 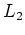 est confondu avec le plan focal image de
est confondu avec le plan focal image de 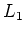 (plan
(plan 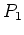 ). Dans ce plan, on place un masque
de coefficient de transmission linéaire en
). Dans ce plan, on place un masque
de coefficient de transmission linéaire en 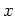
avec 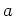 constante réelle. On observe le résultat
du filtrage dans le plan
constante réelle. On observe le résultat
du filtrage dans le plan 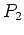 .
.
- S'agit-il d'un filtrage passe-haut ? Passe-bas ? D'une autre nature
(préciser) ?
- Expliquer brièvement pourquoi ce filtrage est appelé
dérivateur.
- Calculer l'amplitude complexe dans le plan
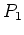 , en déduire
l'amplitude complexe dans le plan
, en déduire
l'amplitude complexe dans le plan 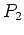 (un formulaire de
TF pourra ètre utile... ou alors une habileté diabolique dans
les calculs d'intégrale !)
(un formulaire de
TF pourra ètre utile... ou alors une habileté diabolique dans
les calculs d'intégrale !)
- L'objet dans le plan
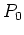 est une fente de largeur
est une fente de largeur 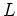 dans la direction
dans la direction 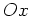 . Décrire l'image dans le plan
. Décrire l'image dans le plan
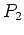 .
.
- Même question si l'objet est est une fente de largeur
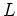 dans la direction
dans la direction 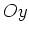 .
.


![]() dans le plan
dans le plan ![]() et de longueur d'onde
et de longueur d'onde
![]() . Les deux lentilles sont de focale
. Les deux lentilles sont de focale ![]() , le plan
focal objet de
, le plan
focal objet de ![]() est confondu avec le plan focal image de
est confondu avec le plan focal image de ![]() (plan
(plan ![]() ). Dans ce plan, on place un masque
de coefficient de transmission linéaire en
). Dans ce plan, on place un masque
de coefficient de transmission linéaire en ![]()