Correction de l'interrogation d'optique
du 21 Octobre 2008
- On se place dans l'hypothèse où
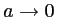 .
.
- Dans ce cas les 2 sinc tendent vers 1 et
avec
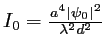 . Cette fonction est maintenant indépendante de
. Cette fonction est maintenant indépendante de 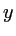 . Le premier cos a pour période
. Le premier cos a pour période
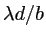 (il correspond aux franges d'interférences des 2 paires de trous distantes de
(il correspond aux franges d'interférences des 2 paires de trous distantes de 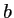 ). Le second cos a une période
). Le second cos a une période
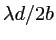 , la moitié du premier (franges d'interférences des deux trous extrêmes distants de
, la moitié du premier (franges d'interférences des deux trous extrêmes distants de 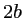 ; comme il n'y a qu'une paire séparée de
; comme il n'y a qu'une paire séparée de 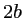 , le second cos a un poids moitié de celui du premier). La période de l'ensemble est donc
, le second cos a un poids moitié de celui du premier). La période de l'ensemble est donc
 .
.
- La dérivée de
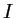 s'écrit
s'écrit
Cette fonction s'anulle 4 fois dans l'intervalle 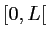 : 2 fois à cause du sinus et 2 fois lorsque le cosinus vaut -1/2. Les 4 positions sont :
: 2 fois à cause du sinus et 2 fois lorsque le cosinus vaut -1/2. Les 4 positions sont :

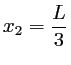
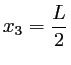
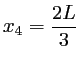
- On constate que
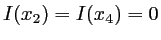 : ce sont donc les positions des franges sombres (intensité nulle, pas de lumière).
: ce sont donc les positions des franges sombres (intensité nulle, pas de lumière).
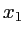 et
et 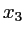 sont donc les positions des franges brillantes. Le calcul donne
sont donc les positions des franges brillantes. Le calcul donne
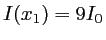 et
et
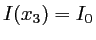 . Il y a donc un maximum principal en
. Il y a donc un maximum principal en 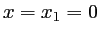 et un maximum secondaire d'intensité 9 fois plus faible en
et un maximum secondaire d'intensité 9 fois plus faible en 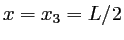
- Graphe de l'intensité
![\includegraphics[width=\textwidth]{figintes.eps}](img28.gif)
![$\displaystyle t(x,y)=\Pi\left(\frac{y}{a}\right)\; \left[\Pi\left(\frac{x}{a}\right)+ \Pi\left(\frac{x-b}{a}\right)+\Pi\left(\frac{x+b}{a}\right)\right]$](img1.gif)
 sinc
sinc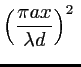 sinc
sinc![$\displaystyle \left(\frac{\pi a y}{\lambda d}\right)^2\: \left[
3+4\cos\left(\f...
...i b x}{\lambda d}\right)+2\cos\left(\frac{4 \pi b x}{\lambda d}\right)
\right]
$](img4.gif)
![$\displaystyle I(x,y)=I_0 \left[
3+4\cos\left(\frac{2 \pi b x}{\lambda d}\right)+2\cos\left(\frac{4 \pi b x}{\lambda d}\right)
\right]
$](img6.gif)
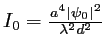 . Cette fonction est maintenant indépendante de
. Cette fonction est maintenant indépendante de 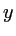 . Le premier cos a pour période
. Le premier cos a pour période
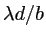 (il correspond aux franges d'interférences des 2 paires de trous distantes de
(il correspond aux franges d'interférences des 2 paires de trous distantes de 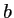 ). Le second cos a une période
). Le second cos a une période
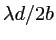 , la moitié du premier (franges d'interférences des deux trous extrêmes distants de
, la moitié du premier (franges d'interférences des deux trous extrêmes distants de 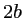 ; comme il n'y a qu'une paire séparée de
; comme il n'y a qu'une paire séparée de 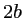 , le second cos a un poids moitié de celui du premier). La période de l'ensemble est donc
, le second cos a un poids moitié de celui du premier). La période de l'ensemble est donc
 .
.
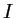 s'écrit
s'écrit
![$\displaystyle I'(x)=-\frac{8\pi}{L}\: \left[\sin\left(\frac{2 \pi x}{L}\right)+...
...\frac{2 \pi x}{L}\right)\: \left[1+2 \cos\left(\frac{2 \pi x}{L}\right)\right]
$](img15.gif)
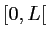 : 2 fois à cause du sinus et 2 fois lorsque le cosinus vaut -1/2. Les 4 positions sont :
: 2 fois à cause du sinus et 2 fois lorsque le cosinus vaut -1/2. Les 4 positions sont :

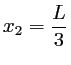
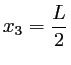
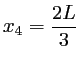
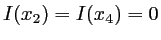 : ce sont donc les positions des franges sombres (intensité nulle, pas de lumière).
: ce sont donc les positions des franges sombres (intensité nulle, pas de lumière).
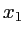 et
et 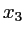 sont donc les positions des franges brillantes. Le calcul donne
sont donc les positions des franges brillantes. Le calcul donne
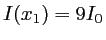 et
et
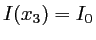 . Il y a donc un maximum principal en
. Il y a donc un maximum principal en 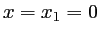 et un maximum secondaire d'intensité 9 fois plus faible en
et un maximum secondaire d'intensité 9 fois plus faible en 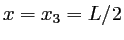
![\includegraphics[width=\textwidth]{figintes.eps}](img28.gif)