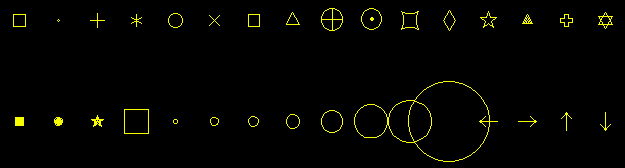
Description de quelques fonctions PGPLOT

Index des fonctions

cpgask(int n)

    Par défaut, les fonctions cpgenv  et cpgend demandent à l'utilisateur de taper <RETURN> avant de passer à la fenètre suivante ou de fermer PgPlot. L'appel de cpgask avant ces fonctions permet de modifier leur comportement :

cpgbeg(int unit, char* dev, int nx, int ny)

    Démarre PgPlot. Voir aussi cpgopen

Arguments :

    unit : Ne sert à rien et vaut toujours 0.
    dev : Le périphérique de sortie graphique. Les valeurs possibles sont :

     nx et ny : Permettent de mettre plusieurs graphes les uns à côyé des autres sur la page. nx est le nombre de graphes dans la direction x (largeur de la page), ny dans la direction y (hauteur de la page).

cpgcirc(float xcent, float ycent, float rayon)

     Dessine un cercle. Le centre du cercle est aux coordonnées (xcent, ycent) et son rayon est donné par la variable rayon. Les trois variables sont en coordonnées utilisateur.

    On peut changer la couleur du cercle par un appel préalable à la fonction cpgsci. De mème un appel préalable cpgsfs  permettra de dessiner un cercle plein, vide ou hachuré.

cpgcont(z, idim, jdim, i1, i2, j1, j2, c, nc, tr)

    float z[ ], c[ ], tr[6];
    int    idim, jdim, i1, i2, j1, j2, nc;

     Dessine les isocontours d'une image (ou fonction de deux variables) ou d'une partie d'une image.

Arguments :

    z : Tableau contenant l'image, de dimension idim*jdim. La structure du tableau z est décrite à la page type des variables .

    idim : Nombre de lignes de l'image
    jdim : Nombre de colonnes de l'image

    i1, i2, j1, j2 : Limites de la sous image à représenter. Si on veut l'image entière, ils valent respectivement 1, idim, 1, jdim.

    nc : Nombre de contours à tracer
    c : Tableau de dimension nc contenant les valeurs des isocontours à tracer

    tr : Tableau de passage permettant de calculer les valeurs (x,y) en coordonnées utilisateur d'un point de l'image se trouvant à la ligne i et la colonne j. Si les coordonnées utilisateur sont simplement les pixels alors tr vaut {1, jdim, 0, 1, 0, idim}. Sinon, PgPlot calcule l' abcisse x et l'ordonnée y d'un pixel à partir de son numéro de ligne i et de son n° de colonne j par la formule :

    x = tr[0] + tr[1]*i + tr[2]*j
    y = tr[3] + tr[4]*i + tr[5]*j

Ce qui donne, dans le cas où il n'y a pas de rotation :

    tr[0]=xmin;
    tr[1]=(xmax-xmin)/jdim;
    tr[2]=0;
    tr[3]=ymin;
    tr[4]=0;
    tr[5]=(ymax-ymin)/idim;

xmin, xmax, ymin et ymax représentant les abcisses et ordonnées maximales et minimales de l'image.

cpgend()

    Ferme PgPlot. Demande à l'utilisateur de taper sur une touche avant de fermer la fenètre graphique, sauf si un cpgask(0) a été demandé auparavant.

cpgenv(xmin, xmax, ymin, ymax, just, axis)

    float xmin, xmax, ymin, ymax;
    int    just, axis;

    Etablit le maximum et le minimum du graphe en abcisse et en ordonnée, calcule la correspondance entre les pixels sur l'écran/imprimante et les coordonnées utilisateur, trace un cadre autour du graphe et les axes.

    La notion de coordonnées utilisateur peut être comprise sur l'exemple suivant : si vous tracez la trajectoire d'un pendule en fonction du temps, vous souhaitez obtenir un graphe theta(t), avec l'axe des temps gradué en secondes et l'axe des theta gradué en radians ou en degrés. t et theta sont les coordonnées utilisateur d'un point sur le graphe.

Arguments :

    xmin, xmax : Abcisses maximum et minimum du graphe (en coordonnées utilisateur) .
   ymin, ymax : Ordonnées maximum et minimum du graphe .

   just : Si just=1, le repère du graphe est orthonormé. Pour toute autre valeur de just, il ne l'est pas.

   axis : Agit sur le tracé du cadre et des axes  :


cpgimag(z, idim, jdim, i1, i2, j1, j2, a1, a2, tr)

    float z[ ];
    int    i1, i2, j1, j2, idim, jdim;
    float a1, a2, tr[6];

     Affiche une image (ou fonction de deux variables) ou une partie d'une image en niveaux de gris ou en fausses couleurs. La palette de couleur peut être changée par un appel préalable à cpgslut

Arguments :

    z : Tableau contenant l'image, de dimension idim*jdim. La structure du tableau z est décrite à la page type des variables .

    idim : Nombre de lignes de l'image
    jdim : Nombre de colonnes de l'image

    i1, i2, j1, j2 : Limites de la sous image à représenter. Si on veut l'image entière, ils valent respectivement 1, idim, 1, jdim.

    a1, a2 : Seuils bas et haut de la représentation. Toute valeur de la fonction inférieure à a1 sera représentée comme si elle était égale à a1, et toute valeur de la fonction supérieure à a2 sera représentée comme si elle était égale à a2. Exemple d'utilisation : pour voir les anneaux faibles d'une tache d'Airy, il faut que a2 soit égal à un centième de la valeur maximale de z.

    tr : Tableau de passage permettant de calculer les valeurs (x,y) en coordonnées utilisateur d'un point de l'image se trouvant à la ligne i et la colonne j. Si les coordonnées utilisateur sont simplement les pixels alors tr vaut {1, jdim, 0, 1, 0, idim}. Sinon, PgPlot calcule l' abcisse x et l'ordonnée y d'un pixel à partir de son numéro de ligne i et de son n° de colonne j par la formule :

    x = tr[0] + tr[1]*i + tr[2]*j
    y = tr[3] + tr[4]*i + tr[5]*j

Ce qui donne, dans le cas où il n'y a pas de rotation :

    tr[0]=xmin;
    tr[1]=(xmax-xmin)/jdim;
    tr[2]=0;
    tr[3]=ymin;
    tr[4]=0;
    tr[5]=(ymax-ymin)/idim;

xmin, xmax, ymin et ymax représentant les abcisses et ordonnées maximales et minimales de l'image.

cpglab(char* xlabel, char* ylabel, char* titre)

    Met un label sur les deux axes et un titre sur le graphe. Les caractères spéciaux (lettres grecques, accents, etc...) sont supportés.

Arguments :

    xlabel : Label  de l'axe des abcisses
    ylabel : Label  de l'axe des ordonnées
    titre : Titre du graphe

cpgline(int n, float* x, float* y)

    Trace une courbe définie sur n points à partir des abcisses x[i] et des ordonnées y[i].

Arguments :

    n : Nombre de points
    x : Tableau des abcisses, dimension n (coordonnées utilisateur)
    y : Tableau des ordonnées

cpgncur(maxpts, npt, x, y, symbol)

    int  maxpts, symbol;
    int  *npt;
    float x[ ], y[ ];

    Permet de sélectionner des points avec la souris. Les abcisses et ordonnées des points sélectionnés seront rangés dans les tableaux x[i] et y[i]. Les points sont rangés dans l'ordre des x croissants.
    On peut sélectionner au maximum maxpt points, on peut aussi en sélectionner moins ; le nombre de points effectivement sélectionné sera rangé dans la variable npt.
    La sélection d'un point se fait en cliquant avec le bouton gauche de la souris. Un symbole s'affiche à la position sélectionnée. Si on s'est trompé, on peut déselectionner un point en cliquant dessus avec le bouton du milieu (ou les deux boutons à la fois si c'est une souris deux boutons).
    Quand on a fini de sélectionner, on clique sur le bouton droit de la souris pour sortir.

Arguments :

    maxpts : Nombre maximum de points à sélectionner
    npt : Au retour, contient le nombre de points sélectionnés
    x : Tableau (dimension maxpts) des abcisses des points sélectionnés
    y : Tableau des ordonnées des points sélectionnés
    symbol : Numéro du symbole à afficher. Les 32 symboles fournis par PgPlot sont sur l'image suivante (de gauche à droite):

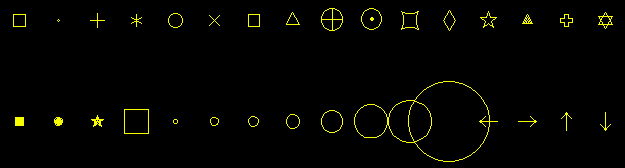
cpgopen(char* dev)

    Démarre PgPlot. Cet appel est équivalent à cpgbeg(0,dev,1,1);
    Voir la documentation sur cpgbeg dpour plus de détails. L'argument dev peut valoir :

cpgrect(float x1, float x2, float y1, float y2)

     Dessine un rectangle. Le coin en bas à gauche est aux coordonnées (x1,y1), le coin en haut à droite aux coordonnées (x2,y2).

    On peut changer la couleur du rectangle par un appel préalable à la fonction cpgsci. De mème un appel préalable cpgsfs  permettra de dessiner un rectangle plein, vide ou hachuré.

cpgscf(int font)

    Change la police de caractères. La police est numérotée par le nombre font. Voici un échantillon des 4 polices diponibles :
 

cpgsch(float taille)

    Change la taille des caractères. taille=1 est la valeur par défaut, taille=2 fait des caractères 2 fois plus gros.

cpgsci(int color)

    Change la couleur du pinceau. Le nombre color indique la couleur, de 0 à 15. Voici un échantillon des 16 couleurs prédéfinies :
 

cpgsfs(int style)

    Change le style de tracé de l'intérieur des polygones. L'argument style peut valoir :


cpgsls(int style)

    Change le style de trait lorsqu'on dessine des lignes. L'argument style peut valoir :

cpgslut(char* nomlut)

    Installe une palette de couleurs lue dans le fichier nomlut sur le disque. Cette fonction s'appelle avant cpgimag. Les palettes de couleur se trouvent dans le répertoire "/users/licence/examples/Graphique/lut"

    Attention : cpgslut n'est pas une fonction standart de PgPlot, c'est un produit maison. Pour l'utiliser, le programme devra comporter, au début,  la ligne suivante :

#include "/users/licence/examples/Graphique/prog/cpgslut.c"

cpgtext(float x, float y, char* texte)

    Affiche un texte contenu dans la chaine de caractères texte aux coordonnées (x,y). Les caractères spéciaux (lettres grecques, accents, etc...) sont supportés.

cpgvect(Ex, Ey, idim, jdim, i1, i2, j1, j2, c, nc, tr, bl)

    float Ex[ ], Ey[ ], tr[6];
    int    idim, jdim, i1, i2, j1, j2, nc;
    float  c, bl;

     Dessine un champ de vecteurs sous la forme de petites flèches. Le champ de vecteurs est dessiné dans un plan (x,y), il possède deux composantes Ex(x,y) et Ey(x,y). Les valeurs de Ex et Ey sont tabulées sur une grille de dimension idim par jdim. Il est recommandé de ne pas excéder 30 pour les valeurs de idim et jdim, sinon le graphe sera illisible (si idim=jdim=30, ca fait une grille de 30x30 petits vecteurs à représenter).

Arguments :

    Ex, Ey : Tableaux contenant les composantes Ex et Ey, de dimension idim*jdim. La structure des tableaux est décrite à la page type des variables .

    idim : Nombre de lignes de Ex et Ey
    jdim : Nombre de colonnes de Ex et Ey

    i1, i2, j1, j2 : Limites de la portion des tableaux Ex et Ey image à représenter. Si on veut la totalité des tableaux Ex et Ey, ils valent respectivement 1,idim,1,jdim.

    nc : Positionnement de la flèche du vecteur. Si i et j représentent la ligne et la colonne du point où les composantes du vecteur sont calculées, alors

    c : Longueur du vecteur. Il est conseillé de mettre la valeur 0 qui correspond à l'intervalle entre deux pas de grille.

    bl : On ne trace pas de flèche si la valeurs de Ex et Ey est égale à bl. Utilisation : lorsque le vecteur devient trop grand (par exemple le champ électrique  au voisinage d'une charge pontuelle), on peut refuser de le dessiner.

  tr : Tableau de passage permettant de calculer les valeurs (x,y) en coordonnées utilisateur d'un point de l'image se trouvant à la ligne i et la colonne j. Si les coordonnées utilisateur sont simplement les pixels alors tr vaut {1, jdim, 0, 1, 0, idim}. Sinon, PgPlot calcule l' abcisse x et l'ordonnée y d'un pixel à partir de son numéro de ligne i et de son n° de colonne j par la formule :

    x = tr[0] + tr[1]*i + tr[2]*j
    y = tr[3] + tr[4]*i + tr[5]*j

Ce qui donne, dans le cas où il n'y a pas de rotation :

    tr[0]=xmin;
    tr[1]=(xmax-xmin)/jdim;
    tr[2]=0;
    tr[3]=ymin;
    tr[4]=0;
    tr[5]=(ymax-ymin)/idim;

xmin, xmax, ymin et ymax représentant les abcisses et ordonnées maximales et minimales de l'image.