CLEM Example
We illustrate LE usage on an industrial example concerning the design of a mecatronics process control: a pneumatic prehensor. We first describe the system working. Then we present the system implementation with LE language. Finally, simulation and verification are detailed.
Pneumatic Prehensor Specification
A pneumatic prehensor takes and assembles cogs and axes. The physical system mainly consists of two double acting pneumatic cylinders and a suction pad. This example has been supplied by an automation specialist group, to experiment new methods of design and analysis of discrete event systems.
Pneumatic Prehensor Design
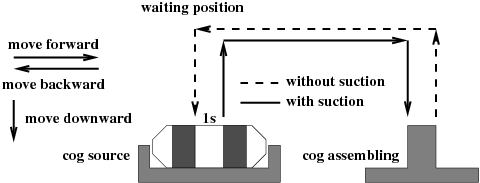
This is the(U cycle) kinematics of the system . Note that the horizontal motion must always be done in the high position.
In what follow we consider the control part of the system.

Incoming information (from the limit switches associated with the cylinders) and outgoing commands (to the pre-actuators).
To implement this application in LE language, we adopt a top down specification technique. At the highest hierarchical level , the controller is the parallel composition of an initialization part followed by the normal cycle running and a temporisation module. This latter is raised by a signal start_tempo and emits a signal end_tempo when the temporisation is over. Of course, these two signals are not in overall interface of the controller, they are only use to establish the communication between the two parallel sides:
module Control:
Input:forward, backward, upward, downward, StartCycle;
Output:MoveFor, MoveBack, MoveDown, SuckUp, EndCycle ;
Run: "./TEST/control/" : Temporisation;
"./TEST/control/" : NormalCycle;
local start_tempo, end_tempo {
wait upward >> emit MoveFor >> wait backward >> run NormalCycle
||
{ run Temporisation}
}
end
The second level of the specification describes temporisation and normal cycle phasis. Both Temporisation and NormalCycle modules are defined in external files. Temporisation module performs a temporisation (waiting for five successive reactions and then emitting a signal end_tempo).
module Transport :
Input: end_tempo, upward, forward, downward;
Output: MoveFor, MoveDown, SuckUp;
local exitTransport {
{ emit MoveDown >> wait end_tempo
>> wait upward >> emit MoveFor
>> wait forward >> emit MoveDown
>> wait downward >> emit exitTransport
}
||
abort
{ loop { pause >> emit SuckUp }}
when exitTransport
}
end
module NormalCycle :
Input: StartCycle, downward, upward, backward,
forward, end_tempo;
Output: start_tempo, MoveDown, MoveBack,
MoveFor, SuckUp, EndCycle;
{ present StartCycle { nothing} else wait StartCycle}
>>
{
loop { emit MoveDown
>> wait downward >> emit start_tempo
>> run Transport
>> wait upward >> emit MoveBack
>> wait backward >> emit EndCycle }
}
end
For instance , we discuss the NormalCycle module implementation. NormalCycle implementation is a loop whose body specifies a single cycle. According to the specification, a single cycle is composed of commands to move the pneumatic cylinders with respect to their positions and a call to a third level of implementation (Transport) to specify the suction pad activity.
|
To compile the overall programs, we performed a separated compilation: first, Temporisation and NormalCycle modules have been compiled and respectively saved in Temporisation.lec and NormalCyle.lec files. Second, the main Control module has been compiled according to our compilation scheme. |
Pneumatic Prehensor Verification
To check the behavior of our implementation with respect to the specification, we first simulate it and then perform model-checking verification.
Simulation
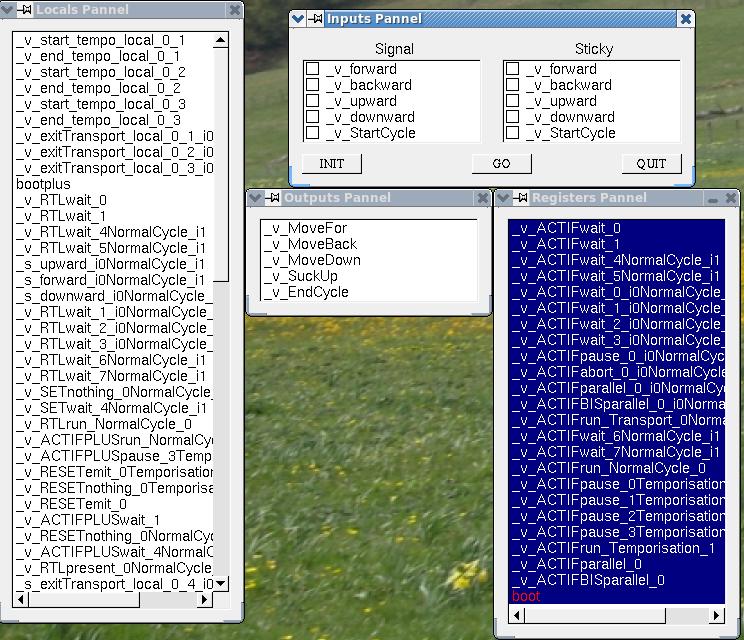
First, we check particular behaviors of main module Control with CLEM simulation tool:
Verification
On another hand, to formally prove safety properties we rely on model checking techniques. In this approach, the correctness of a system with respect to a desired behavior is verified by checking whether a structure that models the system satisfies a formula describing that behavior. Such a formula is usually written by using a temporal logic. Most existing verification techniques are based on a representation of the concurrent system by means of a labeled transition system (LTS). Synchronous languages are well known to have a clear semantic that allows to express the set of behaviors of program as LTSs and thus model checking techniques are available. Then, they rely on formal methods to build dependable software. v
A verification means successfully used for synchronous formalisms is that of observer monitoring. According to this technique, a safety property &phi can be mapped to a program &Omega& which runs in parallel with a program P and observes its behavior, in the sense that at each instant &Omega reads both inputs and outputs of P. If &Omega detects that P has violated &phi then it broadcasts an "alarm" signal. We use such a technique to formally prove Control program behavior.
To verify that the suction is maintained from the instant where the cycle begins up to the cycle ends, the following observer is specified:
module CheckSuckUp;
Input SuckUp, S;
Output exitERROR;
present SuckUp
{ present S {nothing} else {wait S}}
else {pause>>emit exitERROR}
end
module SuctionObs:
Input:forward, backward, upward, downward,
StartCycle, Output:MoveFor, MoveBack,
MoveDown, SuckUp, EndCycle ;
Output: ERROR;
local exitERROR {
abort {
loop {
present StartCycle {nothing} else {wait StartCycle} >>
present MoveDown {nothing} else {wait MoveDown} >>
present downward {nothing} else { wait downward} >>
present MoveDown {nothing}
else { present SuckUp
{run CheckSuckUp[upward\S] >>
run CheckSuckUp[MoveFor\S] >>
run CheckSuckUp[forward\S] >>
run CheckSuckUp[MoveDown\S] >>
wait downward
}
else {emit exitERROR}
}
}
when exitERROR >> emit ERROR
}
}
end
To specify the observer we first define a module (CheckSuckUp) which checks wether the signal SuckUp is present and goes in the state where signal S is present. If SuckUp is absent , exitERROR is emitted. Calling this module, the observer tests the presence of signal SuckUp in each possible states reached when cylinders move.
According to the observer method, we define a LE program which is the parallel composition between the Control module and the observer defined above.
module CheckSuction :
Input: forward, backward, upward, downward, StartCycle;
Output: ERROR;
Run: "/home/ar/GnuStrl/CLEM_SRC/TEST/mecatronics/" : Control;
local MoveFor, MoveBack, MoveDown, SuckUp, EndCycle
{
run Control || run SuctionObs
}
end
To achieve the property checking, we compile the CheckSuction module and we generate the smv code:
clem -main CheckSuction CheckSuction.le -smv
|
We get a CheckSuction.smv file and we load it in NuSMV model checking. We built the NuSMV model for CheckSuction module and we enter the property: : !AG(ERROR) . The answer is true. Thus, ERROR is never emitted and the initial property we want to prove is true. |