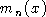 .
. 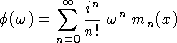
En deux ans et demi de travail sur l'imagerie probabiliste, il m'a été donné de m'intéresser à un spectre assez vaste de problèmes parmi lesquels on peut citer
La finalité de notre travail est d'établir une méthode de reconstruction des images astronomiques dégradées par la turbulence en utilisant des fonctions comme les densités de probabilité ou les fonctions caractéristiques. Ces fonctions contiennent toute l'information à la fois sur les objets observés et sur les champs de speckles eux-mêmes. Les méthodes d'imagerie existantes utilisent actuellement des analyses par moment, moment d'ordre deux pour la speckle interférométrie, la speckle holographie ou la méthode de Knox et Thompson, moment d'ordre trois pour le speckle masking. Les informations contenues dans les moments d'ordre supérieur ne sont pas prises en compte.
L'utilisation de fonction caractéristique permet une analyse simultanée à tous les ordres ; cette fonction peut en effet s'écrire comme un développement en série de Taylor dont les coefficients sont les moments 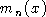 .
.
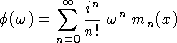
La fonction caractéristique (ou la densités de probabilité qui est sa transformée de Fourier) contient ainsi toute l'information présente dans les moments du deuxième et du troisième ordre, mais aussi celle qui se trouve dans les moments d'ordre supérieur. Appliquée au problème de la reconstruction d'images en astronomie à haute résolution angulaire, son utilisation devrait permettre de fournir des solutions précises, plus encore que le speckle masking. La contrepartie est la difficulté de manipulation de ces fonctions, au niveau théorique à cause des calculs que demande la modélisation aussi bien qu'au niveau du volume de ressources informatiques qui seront nécessaires (les programmes de minimisation de type recuit simulé sont en général très gourmands en temps de calcul machine).
L'organigramme général de l'imagerie probabiliste pourrait être le suivant.
De tous les points de l'organigramme, le modèle gaussien est actuellement celui qui est le plus avancé : nous sommes capables d'écrire la fonction caractéristique de n'importe quel objet vu à travers la turbulence. Ce modèle analytique va cependant être abandonné au profit de celui qui fait intervenir une étoile de référence et qui permet l'estimation de la statistique vraie des champs de speckles observés. En ce qui concerne les algorithmes de restauration, une inversion de la transformée de Poisson par recuit simulé est actuellement en cours de tests (pour le premier ordre), et il est envisagé de passer au second ordre assez prochainement. Le programme de reconstruction d'images par minimisation n'existe pas encore, du moins est-il à l'état de recherches prospectives comme en témoigne le travail qui a été fait sur les étoiles doubles et qui est décrit à la fin du chapitre 2.
L'imagerie probabiliste a déjà commencé à donner des résultats astrophysiques en infrarouge et dans le visible sur des étoiles doubles. Il semble que la méthode soit même assez précise quant à l'estimation des rapports de magnitudes, puisque pour ADS 15281 nous avons eu 4 % d'erreur avec une mesure d'angle relativement grossière sur sa densité de probabilité du second ordre.
Par ailleurs l'utilisation des fonctions statistiques a permis de modéliser par une démarche nouvelle les problèmes qui aparaissent en comptage de photons. Nous avons bien retrouvé l'expressions des biais observés sur les densités spectrales et les bispectres calculés par Dainty et Greenaway [34], et par Wirnitzer [79]. Nous avons aussi appréhendé le problème du clipping qui écrête à 1 le nombre de photons détectés sur un pixel. Ce problème était connu depuis assez longtemps mais on n'en trouve pas de description détaillée dans la littérature ; les résultats que nous avons trouvé montrent c'est un problème qui n'est plus négligeable dès que le flux devient supérieur à photon par pixel. Il limite sérieusement la possibilité d'appliquer des techniques d'ordre supérieur pour renconstruire des images et peut même conduire en speckle interferométrie à des résultats erronnés. Il n'y a pas vraiment de solution à ce problème qui n'est pas linéaire, si ce n'est d'utiliser des caméras qui autorisent une certaine dynamique dans le comptage des photons (CCD bombardés, PAPA, etc...).