Formation d'images en éclairage incohérent

On considère maintenant le problème général : les trous d'Young sont remplacés par un masque quelconque de coefficient de transmission $P(x_1,y_1)$ appelé ``fonction pupille''. Ce masque est placé dans le plan focal objet d'une lentille convergente de focale $F$ . On observe dans le plan focal image de la lentille. Le schéma est le suivant :

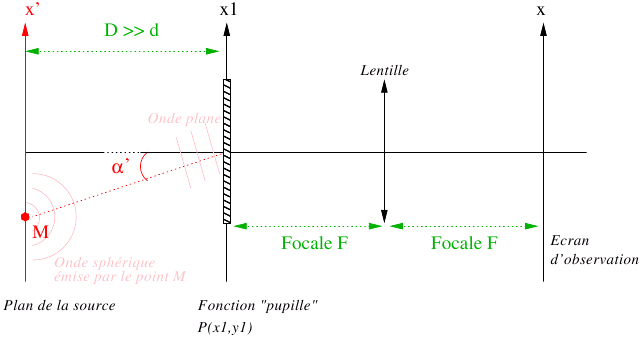
Comme dans le cas du §1.3, on observe une source large placée dans un plan $(x',y',z=-D)$ (avec $D$ suffisamment grand pour faire l'approximation de la diffraction à l'infini). La source est supposée monochromatique (longueur d'onde $\lambda$ ). Le calcul de l'intensité dans le plan focal de la lentille se fait de la même façon que dans le cas des trous d'Young (paragraphe 1.3): on s'intéresse à l'amplitude $df(x,y)$ produite par un point de la source situé dans une direction $(\alpha',\beta')$ , on calcule l'intensité correspondante $dI(x,y)$ et on intègre sur la source.

En utilisant des notations similaires à celle du §1.3, l'amplitude complexe $df_0$ produite dans le plan pupille par le point $M$ est celle d'une onde plane provenant de la direction $(\alpha',\beta')$ . Il vient

$$df_0(x_1,y_1)=K \; d\psi_0\; \exp ik (\alpha' x_1+\beta' y_1)$$

l'amplitude complexe à la sortie du masque est

$$df_1(x_1,y_1)=K \; d\psi_0\; \exp ik (\alpha' x_1+\beta' y_1) . P(x_1,y_1)$$

Pour passer du plan pupille au plan focal image de la lentille, il faut faire une TF optique (voir chapitre ``Filtrage en lumière cohérente''). L'amplitude complexe dans ce plan focal image est donc donnée par

$$df(x,y)=K \; d\psi_0\; \frac{e^{2 i k F}}{i \lambda F} \left[\del... ...ght)\: \ast \: \hat P(u,v)\right]_{u=\frac x{\lambda F}, v=\frac y{\lambda F}}$$

qui se réécrit

$$df(x,y)=K \; d\psi_0\; \frac{e^{2 i k F}}{i \lambda F} \hat P\lef... ...lambda F}-\frac{\alpha'}\lambda,\frac y{\lambda F}-\frac{\beta'}\lambda\right)$$

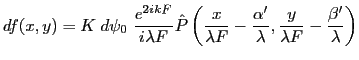
L'intensité correspondante est alors égale à

$$dI(x,y)=dI_0\; \frac{\vert K\vert^2}{\lambda^2 F^2} \left\vert\ha... ...ac{\alpha'}\lambda,\frac y{\lambda F}-\frac{\beta'}\lambda\right)\right\vert^2$$

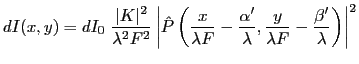
avec $dI_0=O(\alpha',\beta')\, d\alpha'\, d\beta')$ . En posant $\alpha=\frac x F$ et $\beta=\frac y F$ il vient

$$dI(\alpha,\beta)=\frac{\vert K\vert^2}{\lambda^2 F^2} O(\alpha',\... ...(\frac{\alpha - \alpha'}\lambda,\frac{\beta-\beta'}\lambda\right)\right\vert^2$$

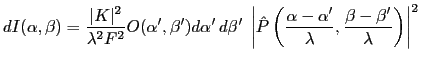
En posant Cte= $\frac{\vert K\vert^2}{\lambda^2 F^2}$ , l'intensité résultant de l'intégrale sur la source ($\alpha'$ et $\beta'$ ) fait apparaitre la relation de convolution objet-image

$$I(\alpha,\beta)=$$   Cte$$\, .\; O(\alpha,\beta)\ast R(\alpha,\beta)$$

avec

$$R(\alpha,\beta)=\left\vert\hat P\left(\frac{\alpha}\lambda,\frac{\beta}\lambda\right)\right\vert^2$$

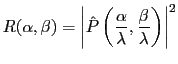
Cette quantité est la réponse impulsionnelle de la formation d'images, c'est l'image qui serait produite par un point-source à l'infini.