Fig. 3.12:
Interféromètre de Michelson.
|
|
Le montage est celui de la figure 3.12. L'onde plane incidente est quasi-monochromatique et se propage parallèlement à l'axe de l'interféromètre (incidence normale). Son spectre est
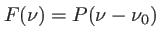 avec
avec 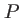 la fonction profil,
la fonction profil, 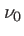 la fréquence centrale et
la fréquence centrale et 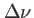 la largeur de
la largeur de 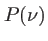 (
(
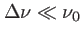 ) . On note
) . On note
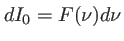 l'intensité de l'onde incidente dans le plan
l'intensité de l'onde incidente dans le plan 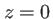 . On appelle
. On appelle 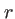 et
et 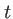 les coefficients de réflexion et transmission en amplitude de la séparatrice. Le miroir
les coefficients de réflexion et transmission en amplitude de la séparatrice. Le miroir 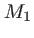 est fixe, le miroir
est fixe, le miroir 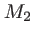 est réglable, son déplacement est noté
est réglable, son déplacement est noté 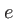 . Le plan d'observation des interférences est parallèle aux plans d'onde des deux ondes incidentes ; l'intensité y sera constante (teinte plate). Pour une position donnée du miroir
. Le plan d'observation des interférences est parallèle aux plans d'onde des deux ondes incidentes ; l'intensité y sera constante (teinte plate). Pour une position donnée du miroir 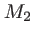 , la différence de marche entre les deux ondes est
, la différence de marche entre les deux ondes est
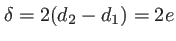 et le retard
et le retard
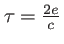 . Les ondes sont toutes deux planes sous incidence normale.
. Les ondes sont toutes deux planes sous incidence normale.
La démarche de calcul des interférences est la même que celle du paragraphe 3.2. On considère l'intensité 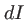 produite dans le plan
produite dans le plan 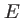 par une tranche
par une tranche
![$ [\nu ,\nu +d\nu ]$](img4.png) , puis on intègre sur la fréquence. Il vient
, puis on intègre sur la fréquence. Il vient
qui s'écrit, en fonction du retard 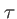 et de la fréquence
et de la fréquence 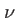
C'est la même formule que dans le cas des trous d'Young (équation 3.1). L'intégrale sur la fréquence conduit donc à la même expression pour l'intensité totale dans le plan 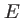 :
:
Cette expression de l'intensité est en fait générale lorqu'on l'exprime en fonction du retard 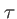 . Pour les franges d'Young
. Pour les franges d'Young
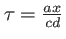 , pour l'interféromètre de Michelson
, pour l'interféromètre de Michelson
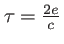 . On pourrait imaginer d'autres dispositifs produisant des interférences à deux ondes planes (miroir de Lloyd, biprisme de Fresnel...) dans lequel le retard
. On pourrait imaginer d'autres dispositifs produisant des interférences à deux ondes planes (miroir de Lloyd, biprisme de Fresnel...) dans lequel le retard 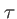 s'exprimerait en fonction des variables du problème. Mais la forme générale de l'intensité en fonction de
s'exprimerait en fonction des variables du problème. Mais la forme générale de l'intensité en fonction de 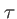 resterait la même si les deux ondes sont de même amplitude (ce ne serait plus le cas pour deux trous d'Young de diamètre différents conduisant à une onde plus lumineuse que l'autre).
resterait la même si les deux ondes sont de même amplitude (ce ne serait plus le cas pour deux trous d'Young de diamètre différents conduisant à une onde plus lumineuse que l'autre).
Prenons pour 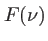 une fonction porte de largeur
une fonction porte de largeur 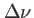 centrée sur la fréquence
centrée sur la fréquence 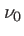 .
.
La fonction profil est ici
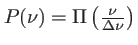 . L'intensité s'exprime, en faisant le changement de variable
. L'intensité s'exprime, en faisant le changement de variable
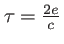 et en posant
et en posant
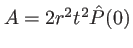 :
:
On observe bien une intensité uniforme (dite ``teinte plate'') dans le champ d'interférences. Faire varier 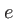 change la luminosité de la teinte plate comme illustré sur la figure 3.13.
change la luminosité de la teinte plate comme illustré sur la figure 3.13.
Fig. 3.13:
Interféromètre de Michelson: variation de l'intensité de la teinte plate en fonction de la différence de marche 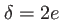 . Le profil de raie est une porte de largeur
. Le profil de raie est une porte de largeur 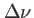 . L'enveloppe des oscillations (fonction contraste) est un sinuus cardinal.
. L'enveloppe des oscillations (fonction contraste) est un sinuus cardinal.
|
|
Le Michelson utilisé dans cette configuration est un spectromètre à transformée de Fourier. En effet, il est possible de mesurer l'allure du profil de raie de la lumière incidente en procédant comme suit :
- On part de
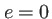 et on mesure
et on mesure 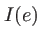 pour
pour 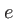 variant par pas de
variant par pas de 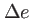 (on dit qu'on scanne la différence de marche). On obtient la courbe
(on dit qu'on scanne la différence de marche). On obtient la courbe 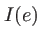 .
.
- Par changement de variable
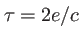 on obtient
on obtient 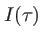 .
.
- On en déduit la fonction contraste
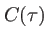 .
.
- Par transformée de Fourier inverse on en déduit
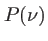 (à la constante
(à la constante 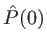 près. Celà marche si le profil de raie
près. Celà marche si le profil de raie 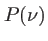 est symétrique (sinon on obtiendra un profil ``symétrisé'' proportionnel à
est symétrique (sinon on obtiendra un profil ``symétrisé'' proportionnel à
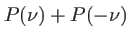 qui apporte quand même des informations sur la forme de la raie).
qui apporte quand même des informations sur la forme de la raie).
![\includegraphics[width=12cm]{eps/interf_michels.eps}](img147.png)
![]() produite dans le plan
produite dans le plan ![]() par une tranche
par une tranche
![]() , puis on intègre sur la fréquence. Il vient
, puis on intègre sur la fréquence. Il vient
![$\displaystyle dI \; = \; = \; 2r^2t^2 F(\nu) d\nu \; \left[1+ \cos\left(\frac{2 \pi 2e}{\lambda}\right)\right]
$](img158.png)
![$\displaystyle I(\tau)=2r^2t^2 \hat P(0)\:\left[1 +\frac{\vert\hat P(\tau)\vert}{\hat P(0)} \cos(2 \pi \nu_0\tau-\phi(\tau))\right]
$](img160.png)
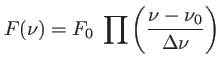
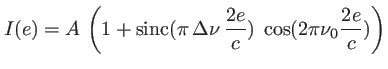
![\includegraphics[width=12cm]{eps/michel_spectf.eps}](img165.png)