Interprétation - Définition de la cohérence
1. Si les fréquences 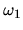 et
et 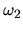 sont égales
sont égales
C'est alors l'interférence entre deux ondes planes monochromatiques,
le problème est identique à celui d'une onde plane monochromatique
ayant traversé l'interféromètre de Michelson. L'intensité
moyenne s'écrit
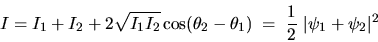
Le terme d'interférences fait intervenir la différence
de phase 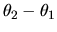 .
Dans le cas du Michelson,
.
Dans le cas du Michelson, 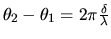 où
où 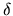 est la différence de trajet entre les deux ondes qui interfèrent.
On dit dans ce cas que les deux ondes sont cohérentes entre elles.
En général on oubliera le facteur
est la différence de trajet entre les deux ondes qui interfèrent.
On dit dans ce cas que les deux ondes sont cohérentes entre elles.
En général on oubliera le facteur 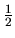 et on écrira
et on écrira
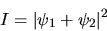
2. Si les fréquences 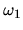 et
et 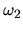 sont pratiquement égales
sont pratiquement égales
On est dans le cas où 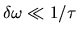 .
Le résultat est identique au cas monochromatique et l'intensité
moyenne s'écrit
.
Le résultat est identique au cas monochromatique et l'intensité
moyenne s'écrit
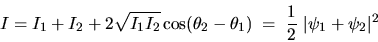
3. Si les fréquences 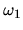 et
et 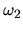 sont très différentes
sont très différentes
C'est le cas où 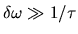 .
Dans ce cas
.
Dans ce cas 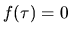 et l'intensité moyenne s'écrit
et l'intensité moyenne s'écrit
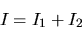
Le terme d'interférences a disparu, l'intensité moyenne
est la somme des intensités moyennes des deux ondes. On dit dans
ce cas que les deux ondes sont incohérentes entre elles.
Ce cas correspond à une différence de phase 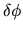 entre les deux ondes qui varie dans le temps :
entre les deux ondes qui varie dans le temps :
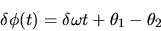
C'est la différence essentielle avec le cas où les deux
ondes sont cohérentes entre elles.
4. Le cas intermédiaire
On parle alors de cohérence partielle entre les deux ondes.
Ce cas se réalise lorsque 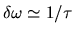 .
En fait cette condition n'est jamais atteinte en lumière visible
: les valeurs typiques de
.
En fait cette condition n'est jamais atteinte en lumière visible
: les valeurs typiques de 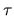 sont de l'ordre de 1/100 de seconde, donc la cohérence partielle
est réalisée lorsque
sont de l'ordre de 1/100 de seconde, donc la cohérence partielle
est réalisée lorsque 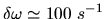 .
Les fréquences optiques sont de l'ordre de
.
Les fréquences optiques sont de l'ordre de 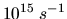 .
Ce qui donne des différences relatives de longueur d'onde
.
Ce qui donne des différences relatives de longueur d'onde
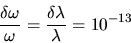
Les longueurs d'onde optique étant de l'ordre de la fraction
de micron, il faut donc pour avoir cohérence partielle que
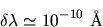
Ce qui est impossible à réaliser même avec des lasers
très ``monochromatiques'' qui possèdent une largeur de raie
(et donc une incertitude sur leur longueur d'onde) de l'ordre de 0.01 Å.
On ne peut donc pas faire interférer des ondes planes issues de
sources différentes, l'accord de 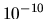 Å en longueur d'onde étant impossible à réaliser.
C'est pour cette raison que les montages optiques (trous d'Young, Michelson,
...) font toujours interférer deux parties d'une même onde.
Å en longueur d'onde étant impossible à réaliser.
C'est pour cette raison que les montages optiques (trous d'Young, Michelson,
...) font toujours interférer deux parties d'une même onde.
En résumé
-
On dira que deux ondes sont cohérentes entre elles si elles
présentent une différence de phase stationnaire
-
Lorsque deux ondes sont cohérentes, l'intensité moyenne
est le carré du module de la somme des amplitudes complexes.
-
Lorsque deux ondes sont incohérentes, l'intensité moyenne
est la somme des intensités moyennes des deux ondes.
Suivant : Cohérence temporelle Précédent
: Cohérence
mutuelle
![]() .
Dans le cas du Michelson,
.
Dans le cas du Michelson, ![]() où
où ![]() est la différence de trajet entre les deux ondes qui interfèrent.
On dit dans ce cas que les deux ondes sont cohérentes entre elles.
En général on oubliera le facteur
est la différence de trajet entre les deux ondes qui interfèrent.
On dit dans ce cas que les deux ondes sont cohérentes entre elles.
En général on oubliera le facteur ![]() et on écrira
et on écrira
![]() entre les deux ondes qui varie dans le temps :
entre les deux ondes qui varie dans le temps :
![]() Å en longueur d'onde étant impossible à réaliser.
C'est pour cette raison que les montages optiques (trous d'Young, Michelson,
...) font toujours interférer deux parties d'une même onde.
Å en longueur d'onde étant impossible à réaliser.
C'est pour cette raison que les montages optiques (trous d'Young, Michelson,
...) font toujours interférer deux parties d'une même onde.