Interférence de deux ondes planes de fréquences différentes
-- Notion de cohérence mutuelle
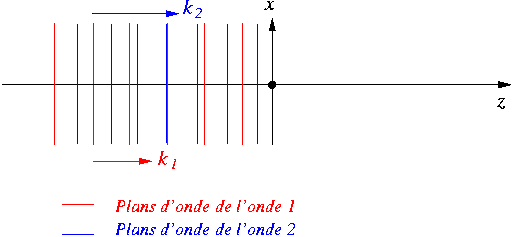
On considère deux ondes planes 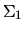 et
et 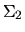 de pulsations
de pulsations 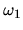 et
et 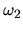 ,
de vecteurs d'onde
,
de vecteurs d'onde 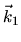 et
et 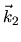 se propageant toutes deux parallèlement à l'axe
se propageant toutes deux parallèlement à l'axe 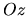 .
On note
.
On note 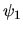 et
et 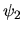 les amplitudes complexes des deux ondes et on s'intéresse à
l'intensité moyenne observée en un point
les amplitudes complexes des deux ondes et on s'intéresse à
l'intensité moyenne observée en un point 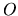 pris comme origine des coordonnées.
pris comme origine des coordonnées.
On pose
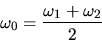
et
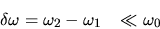
Au point 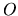 les amplitudes complexes s'écrivent
les amplitudes complexes s'écrivent
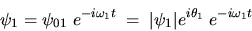
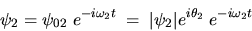
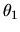 et
et 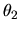 représentent les phases de
représentent les phases de 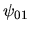 et
et 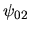 .
.
Calcul de l'intensité instantannée
L'intensité instantannée 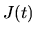 au point
au point 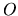 est proportionnelle au carré du champ électrique, donc au
carré de la somme des parties réelles des amplitudes complexes
des deux ondes :
est proportionnelle au carré du champ électrique, donc au
carré de la somme des parties réelles des amplitudes complexes
des deux ondes :
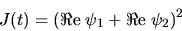
Ce qui s'écrit, en remarquant que 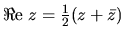 :
:
![\begin{displaymath}J(t)={\Re}\mbox{e}\;[\psi_1]^2+{\Re}\mbox{e}\;[\psi_2]^2 + {......box{e}\;[\psi_1 \psi_2] + {\Re}\mbox{e}\;[\psi_1 \bar{\psi}_2]\end{displaymath}](img123.gif)
Il vient la somme de quatre termes
![\begin{displaymath}\begin{array}{lcll}J(t) & = & \displaystyle \vert\psi_{1}\v......ega_1) t+\theta_1-\theta_2] & \mbox{ \it terme (4)}\end{array}\end{displaymath}](img124.gif)
L'intensité moyenne 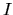
Elle s'écrit comme la moyenne sur le temps de pose 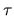 du détecteur utilisé. Nous la noterons ainsi
du détecteur utilisé. Nous la noterons ainsi
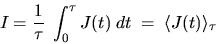
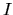 est la somme des moyennes des quatre termes intervenant dans
est la somme des moyennes des quatre termes intervenant dans 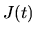 .
En lumière visible, les fréquences sont de l'ordre de
.
En lumière visible, les fréquences sont de l'ordre de 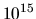 Hz et les temps de pose des détecteurs varient entre la milliseconde
et la seconde.
Hz et les temps de pose des détecteurs varient entre la milliseconde
et la seconde. 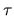 contient alors typiquement
contient alors typiquement 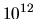 périodes de
périodes de 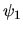 et
et 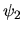 .
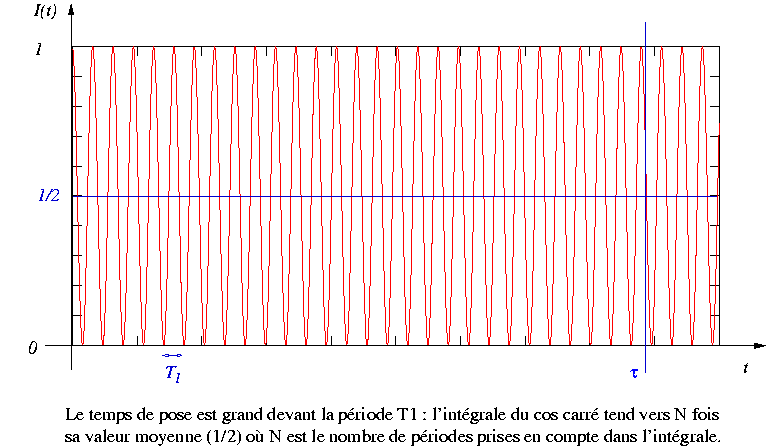
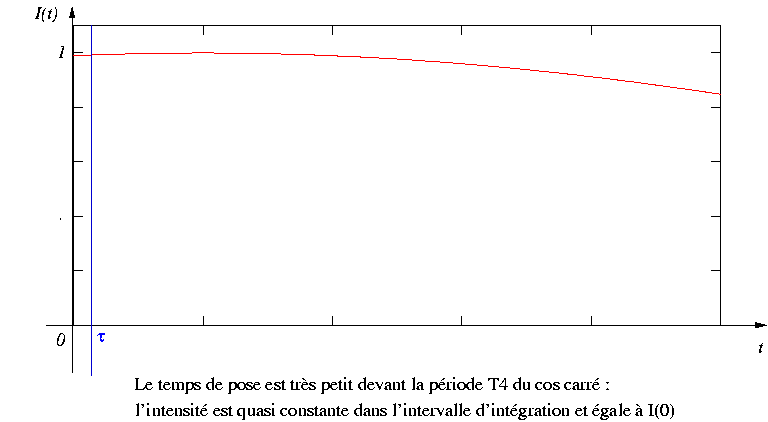
Examinons l'effet de la valeur moyenne sur chacun des termes de
.
Examinons l'effet de la valeur moyenne sur chacun des termes de 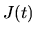 .
.
L'intensité moyenne au point 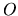 s'écrit alors comme la somme de trois termes
s'écrit alors comme la somme de trois termes
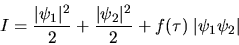
ou
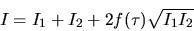
avec
-
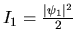 l'intensité moyenne de l'onde
l'intensité moyenne de l'onde 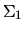 .
.
-
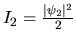 est l'intensité moyenne de l'onde
est l'intensité moyenne de l'onde 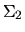 .
.
-
Le terme croisé
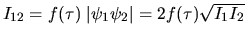 est l' intensité mutuelle. C'est lui qui contient les interférences
entre les deux ondes. Il dépend de leur différence de phase.
est l' intensité mutuelle. C'est lui qui contient les interférences
entre les deux ondes. Il dépend de leur différence de phase.
Suivant : Interprétation
Précédent : Trous
d'Young


![]() les amplitudes complexes s'écrivent
les amplitudes complexes s'écrivent
![]() et
et ![]() représentent les phases de
représentent les phases de ![]() et
et ![]() .
.
![]() :
:
![\begin{displaymath}\begin{array}{lcll}J(t) & = & \displaystyle \vert\psi_{1}\v......ega_1) t+\theta_1-\theta_2] & \mbox{ \it terme (4)}\end{array}\end{displaymath}](img124.gif)
![]() est la somme des moyennes des quatre termes intervenant dans
est la somme des moyennes des quatre termes intervenant dans ![]() .
En lumière visible, les fréquences sont de l'ordre de
.
En lumière visible, les fréquences sont de l'ordre de ![]() Hz et les temps de pose des détecteurs varient entre la milliseconde
et la seconde.
Hz et les temps de pose des détecteurs varient entre la milliseconde
et la seconde. ![]() contient alors typiquement
contient alors typiquement ![]() périodes de
périodes de ![]() et
et ![]() .
Examinons l'effet de la valeur moyenne sur chacun des termes de
.
Examinons l'effet de la valeur moyenne sur chacun des termes de ![]() .
.