Licence de Physique -- Devoir d'optique
Interféromètre de Michelson1
Pour le 23 Avril 2001
Dans tout le sujet, sauf la partie 9
qui concerne la polarisation, on se place dans l'approximation de l'optique
: la grandeur qui se propage est assimilée à un scalaire.
1. Questions préliminaires
On se place ici dans la cas idéal de deux sources lumineuses 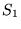 et
et 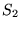 ponctuelles monochromatiques, de même longueur d'onde
ponctuelles monochromatiques, de même longueur d'onde  et de même intensité
et de même intensité  .
On pose
.
On pose 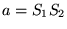 et on appelle
et on appelle 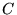 le milieu du segment
le milieu du segment  .
.
-
Exprimer l'intensité lumineuse en
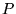 en fonction de
en fonction de  et
et 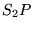 et en déduire la forme générale des surfaces d'égale
intensité.
et en déduire la forme générale des surfaces d'égale
intensité.
On utilise maintenant un écran 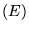 et on appelle axe du système la droite
et on appelle axe du système la droite  normale à l'écran. On se place dans l'approximation de Gauss
(interférences en un point
normale à l'écran. On se place dans l'approximation de Gauss
(interférences en un point 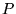 proche de l'axe).
proche de l'axe).

-
Les sources
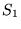 et
et 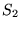 sont sur l'axe (fig. 1). Pourquoi les franges d'interférences sont-elles
des anneaux ? Calculer le rayon
sont sur l'axe (fig. 1). Pourquoi les franges d'interférences sont-elles
des anneaux ? Calculer le rayon 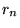 de la frange numéro
de la frange numéro  (
( étant le centre). On pourra noter
étant le centre). On pourra noter 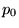 l'ordre d'interférence (rapport de la différence de marche
à la longueur d'onde), supposé entier au point
l'ordre d'interférence (rapport de la différence de marche
à la longueur d'onde), supposé entier au point 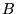 .
Quelle est la fréquence spatiale locale de la figure d'interférences
au point
.
Quelle est la fréquence spatiale locale de la figure d'interférences
au point 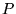 de coordonnées
de coordonnées  sur l'écran
sur l'écran 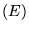 ?
?
-
Les sources
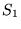 et
et 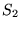 sont perpendiculaires l'axe (fig. 2). Ecrire l'intensité au point
sont perpendiculaires l'axe (fig. 2). Ecrire l'intensité au point 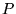 .
Quelle est la forme des franges ? Quelle est la fréquence spatiale
locale de la figure d'interférences ? En déduire l'interfrange
au voisinage de
.
Quelle est la forme des franges ? Quelle est la fréquence spatiale
locale de la figure d'interférences ? En déduire l'interfrange
au voisinage de 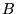 .
.
-
Les sources
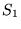 et
et 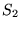 sont maintenant à l' ``infini''. Montrer dans ce cas que les deux
ondes qui interfèrent sont planes de vecteurs d'onde
sont maintenant à l' ``infini''. Montrer dans ce cas que les deux
ondes qui interfèrent sont planes de vecteurs d'onde 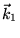 et
et  .
Exprimer l'intensité au point
.
Exprimer l'intensité au point 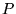 .
.
La suite du problème est consacrée à l'interféromètre
de Michelson
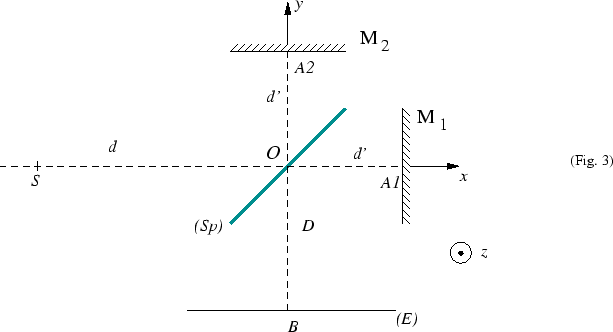
L'interféromètre (fig. 3) est constitué de
-
2 miroirs réglables
 et
et  .
.  peut se déplacer parallèlement à
peut se déplacer parallèlement à  .
.
-
une lame séparatrice semi-réfléchissante
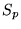 qui réfkéchit la moitié de la lumière qu'elle
reçoit. Cette lame est placée en
qui réfkéchit la moitié de la lumière qu'elle
reçoit. Cette lame est placée en 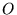 et fait un angle de 45
et fait un angle de 45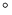 avec
avec  .
.
Dans un premier temps, on suppose que l'épaisseur de la séparatrice
est négligeable et qu'elle n'introduit aucun déphasage ;
on n'envisage pas de lame compensatrice. L'interféromètre
est dit ``réglé'' lorsque  est exactement orthogonal à
est exactement orthogonal à  et
et  à
à 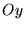 ,
et que les deux miroirs sont symétriques par rapport à
,
et que les deux miroirs sont symétriques par rapport à 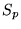 .
Les deux miroirs peuvent pivoter autour des axes
.
Les deux miroirs peuvent pivoter autour des axes 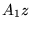 et
et  .
L'écran
.
L'écran 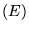 est placé perpendiculairement à
est placé perpendiculairement à 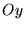 .
On pose
.
On pose  .
.
On dispose de trois lentilles convergentes 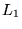 ,
, 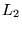 et
et  de focales 5 mm, 20 cm et 1 m respectivement.
de focales 5 mm, 20 cm et 1 m respectivement.
2. Interféromètre
utilisé avec une source ponctuelle
Une source ponctuelle monochromatique de longueur d'onde  est placée en
est placée en  sur l'axe
sur l'axe  .
On pose
.
On pose  .
.
-
Comment peut-on obtenir simplement une telle source à partir d'un
laser et de lentille(s) ?
-
On part de l'interféromètre réglé avec
 cm et on déplace
cm et on déplace  par translation d'une distance
par translation d'une distance 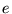 dans la direction des
dans la direction des  croissants.
croissants.
-
Faire une figure soignée et montrer qu'on observe alors des franges
d'interférence en précisant la position des sources secondaires
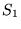 et
et 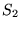 .
.
-
Quelle est leur forme géométrique ? Calculer le rayon sur
l'écran des trois premières franges sombres. A.N.:
 cm,
cm,  cm,
cm,  mm,
mm, 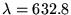 nm.
nm.
-
Montrer qu'on peut obtenir géométriquement les sources secondaires
en utilisant la source primaire et les miroirs
 et
et  (
( est l'image de
est l'image de  par rapport à la séparatrice).
par rapport à la séparatrice).
-
On part à nouveau de l'interféromètre réglé
et on fait tourner
 autour de
autour de 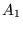 d'un angle
d'un angle  petit.
petit.
-
Faire une figure soignée et montrer qu'on observe alors des franges
d'interférence, en précisant la position des sources secondaires
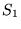 et
et 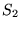 .
Quelle est leur forme géométrique ? Calculer la position
sur l'écran des franges sombres. Faire l'application numérique
pour
.
Quelle est leur forme géométrique ? Calculer la position
sur l'écran des franges sombres. Faire l'application numérique
pour  cm,
cm,  cm,
cm,  minutes,
minutes,  nm.
nm.
On suppose que les miroirs gardent la même position dans la
suite de la question 2-3
-
On remplace la source ponctuelle par une fente très fine. Comment
faut-il disposer celle-ci pour obtenir des interférences sur l'écran
?
-
A partir du cas précédent, on élargit maintenant la
fente de façon symétrique en lui donnant une largeur
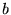 .
Montrer, en supposant que la source est uniformément éclairée
de manière incohérente sur sa largeur, qu'on a une superposition
continue de systèmes d'interférences, ce qui conduit à
une diminution du contraste. Exprimer l'intensité lumineuse sur
l'écran. Comment définir le contraste en fonction de
.
Montrer, en supposant que la source est uniformément éclairée
de manière incohérente sur sa largeur, qu'on a une superposition
continue de systèmes d'interférences, ce qui conduit à
une diminution du contraste. Exprimer l'intensité lumineuse sur
l'écran. Comment définir le contraste en fonction de 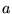 ,
, 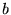 et des autres données ? Justifier le terme ``contraste'' utilisé
à propos de la grandeur ainsi définie. A.N.:
et des autres données ? Justifier le terme ``contraste'' utilisé
à propos de la grandeur ainsi définie. A.N.:  mm : caculer le contraste des franges.
mm : caculer le contraste des franges.
-
Qu'appelle-t'on cohérence spatiale d'une source ? En utilisant les
résultats de la question précédente, définir
et calculer la largeur de cohérence de la fente.
-
Peut-on obtenir des interférences quelle que soit la largeur de
la fente source ?
3. Interféromètre
utilisé avec une source large
On utilise un interféromètre réglé et on déplace  d'une distance
d'une distance 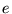 dans le sens des
dans le sens des  croissants.
croissants.
-
On considère une direction de rayons issus de la source caractérisée
par l'angle
 avec l'axe
avec l'axe  .
Montrer qu'un tel rayon, dédoublé par la séparatrice,
donnera à la sortie un ensemble de deux rayons parallèles.
.
Montrer qu'un tel rayon, dédoublé par la séparatrice,
donnera à la sortie un ensemble de deux rayons parallèles.
-
Calculer la différence de marche
 entre ces deux rayons.
entre ces deux rayons.
-
Montrer qu'en plaçant en un point de l'axe
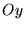 une lentille convergente
une lentille convergente  de focale
de focale 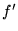 ,
les franges d'interférences s'observent dans plan focal image de
,
les franges d'interférences s'observent dans plan focal image de  .
Quelle est leur forme ?
.
Quelle est leur forme ?
-
Application numérique : calculer les caractéristiques géométriques
des deux premières franges sombres obtenues avec une source de longueur
d'onde
 =546
nm, pour
=546
nm, pour 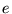 =0.5
mm et en utilisant la lentille
=0.5
mm et en utilisant la lentille  de focale
de focale 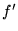 =1
m.
=1
m.
-
La largeur de la source intervient-elle sur le contraste des anneaux ?
Que détermine-t'elle ?
-
Décrire les phénomènes observés lorsqu'on déplace
lentement
 dans le sens des
dans le sens des  décroissants.
décroissants.
-
Comment doit-on choisir les lentilles à utiliser dans les cas suivants
:
-
On cherche à présenter le phénomène à
toute une classe
-
On désire enregistrer un interférogramme
Justifiez votre réponse.
4. Interférogrammes obtenus
avec diverses radiations
On motorise le déplacement du miroir  .
Sa translation se fait alors à vitesse constante
.
Sa translation se fait alors à vitesse constante  .
On appelle
.
On appelle 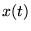 l'abcisse du point
l'abcisse du point 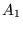 sur l'axe
sur l'axe  .
A l'instant initial,
.
A l'instant initial,  .
Dans le plan focal de la lentille de projection
.
Dans le plan focal de la lentille de projection 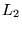 ,
une photodiode placée sur l'axe
,
une photodiode placée sur l'axe 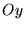 délivre un photocourant
délivre un photocourant  proportionnel à l'intensité lumineuse reçue. Un enregistreur
permet de tracer la courbe
proportionnel à l'intensité lumineuse reçue. Un enregistreur
permet de tracer la courbe  .
.
-
On éclaire l'interféromètre par un laser de longueur
d'onde
 =632.8
nm. Tracer l'allure de l'interférogramme
=632.8
nm. Tracer l'allure de l'interférogramme  obtenu. Quelle est sa période temporelle
obtenu. Quelle est sa période temporelle  ?
?
-
On utilise maintenant une lampe à vapeur de mercure munie d'un filtre
interférentiel laissant passer le doublet jaune du mercure constitué
de deux radiations de même intensité, de loingueurs d'onde
 =577
nm,
=577
nm, 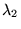 =579
nm, soit
=579
nm, soit 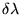 =2
nm. Tracer l'allure de l'interférogramme
=2
nm. Tracer l'allure de l'interférogramme  .
Sur cet interférogramme, dégager deux temps caractéristiques
:
.
Sur cet interférogramme, dégager deux temps caractéristiques
:  analogue à celui de la question précédente, et
analogue à celui de la question précédente, et 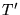 .
Les relier aux caractéristiques des radiations étudiées
et à la vitesse
.
Les relier aux caractéristiques des radiations étudiées
et à la vitesse  .
Que vaut numériquement
.
Que vaut numériquement 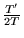 ? Que représente ce nombre ?
? Que représente ce nombre ?
-
En fait les deux composantes du doublet jaune du mercure sont mieux modélisées
par des raies lorentziennes de même profil (c'est à dire de
même intensité et de même largeur spectrale
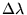 =0.1
nm) centrées sur les nombres d'ondes
=0.1
nm) centrées sur les nombres d'ondes  et
et  .
Pour la raie 1, la distribution spectrale d'intensité (donnée
en fonction de
.
Pour la raie 1, la distribution spectrale d'intensité (donnée
en fonction de 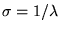 )
peut s'écrire
)
peut s'écrire
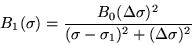
Même chose pour la raie 2 en remplaçant  par
par  .
Les deux largeurs
.
Les deux largeurs  sont supposées identiques.
sont supposées identiques.
-
On suppose pour commencer que l'interféromètre est éclairé
par la seule raie 1. Déterminer le photocourant en fonction de la
différence de marche
 .
Exprimer en fonction de
.
Exprimer en fonction de  et des autres données le temps caractéristique
et des autres données le temps caractéristique  de la décroissance de l'enveloppe
de la décroissance de l'enveloppe  .
.
-
L'interféromètre est maintenant éclairé par
les deux raies du doublet. Donner l'allure de l'interférogramme
 obtenu en évaluant le rapport
obtenu en évaluant le rapport  .
Proposer une méthode expérimentale pour mesurer la largeur
spectrale des composantes du doublet jaune du mercure.
.
Proposer une méthode expérimentale pour mesurer la largeur
spectrale des composantes du doublet jaune du mercure.
-
A votre avis, quel est le phénomène physique qui permet de
justifier que le profil des raies d'une lampe spectrale peut effectivement
être modélisé par une lorentzienne ? Connaissez-vous
d'autres phénomènes qui peuvent contribuer à la largeur
des raies ?
-
C'est l'enregistreur qui impose une limitation pour la vitesse de translation
 du fait de son temps de réponse. Sachant que ce temps est de 0.05
s, calculer la vitesse
du fait de son temps de réponse. Sachant que ce temps est de 0.05
s, calculer la vitesse  correspondante. La vis micrométrique entrainant la translation a
un pas de 0.5 mm et fait un tour en dix minutes. La condition précédente
est-elle vérifiée ?
correspondante. La vis micrométrique entrainant la translation a
un pas de 0.5 mm et fait un tour en dix minutes. La condition précédente
est-elle vérifiée ?
5. Franges d'égale épaisseur
L'interféromètre étant réglé, on fait
tourner le miroir  autour de
autour de 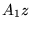 d'un angle
d'un angle  faible. Il est alors réglé en ``coin d'air''. On éclaire
avec un laser (
faible. Il est alors réglé en ``coin d'air''. On éclaire
avec un laser ( =632.8
nm) muni d'un élargisseur de faisceau donnant un pinceau de rayons
sensiblement parallèles.
=632.8
nm) muni d'un élargisseur de faisceau donnant un pinceau de rayons
sensiblement parallèles.
-
Caractériser les interférences obtenues avec ce dispositif.
Comment peut-on les observer ? Où doit-on placer l'écran
? Comment doit-on choisir la lentille qui permet d'obtenir des franges
bien visibles sur l'écran ? Quelle est la forme et la disposition
de ces franges ?
-
On choisit
 .
Comment peut-on le plus commodément, à l'aide d'une des lentilles
.
Comment peut-on le plus commodément, à l'aide d'une des lentilles 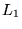 ,
, 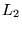 ou
ou  obtenir des franges distantes de 2 mm sur l'écran
obtenir des franges distantes de 2 mm sur l'écran 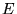 en conservant
en conservant 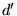 =10
cm ? A quelle distance de
=10
cm ? A quelle distance de 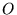 doit-on placer cette lentille et l'écran
doit-on placer cette lentille et l'écran 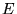 ?
?
-
La source est toujours monochromatique. On la place dans le plan focal
d'une lentille convergente de focale
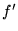 =10
cm. Mais cette fente possède une certaine largeur géométrique
=10
cm. Mais cette fente possède une certaine largeur géométrique 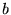 ,
ce qui fait que tous les rayons qui en sont issus n'ont pas le même
angle d'incidence.
,
ce qui fait que tous les rayons qui en sont issus n'ont pas le même
angle d'incidence.
-
Donner les composantes des vecteurs d'onde
 et
et  des rayons qui interfèrent après réflexion sur les
miroirs
des rayons qui interfèrent après réflexion sur les
miroirs  et
et  ,
en notant
,
en notant  l'angle d'incidence sur
l'angle d'incidence sur  .
.
-
En déduire l'intensité lumineuse et déterminer la
valeur de
 donnant aux franges le meilleur contraste possible.
donnant aux franges le meilleur contraste possible.
-
Evaluer la largeur
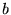 maximale admissible pour conserver 500 franges bien contrastées
et disposées de part et d'autre de l'ordre zéro.
maximale admissible pour conserver 500 franges bien contrastées
et disposées de part et d'autre de l'ordre zéro.
-
A l'aide d'une lampe à vapeur de Sodium on éclaire maintenant
une fente fine qui sert donc de source et qui est placée dans le
plan focal objet d'une lentille convergente de focale 10 cm. On suppose
que la lampe délivre uniquement deux radiations de même intensité
et de longueurs d'onde
 =589.0
nm et
=589.0
nm et 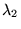 =589.6
nm (doublet du Sodium).
=589.6
nm (doublet du Sodium).
-
Comment doit-on disposer cette fente pour obtenir des franges bien contrastées
?
-
On translate le miroir
 dans la direction
dans la direction  .
Décrire les phénomènes observés. De combien
faut-il déplacer
.
Décrire les phénomènes observés. De combien
faut-il déplacer  pour retrouver exactement le même contraste ?
pour retrouver exactement le même contraste ?
6. Interférences en lumière
blanche
Comme précédemment, l'interféromètre est soigneusement
réglé et on a fait tourner le miroir  d'un angle
d'un angle  faible. On utilise une lampe délivrant de la lumière blanche.
faible. On utilise une lampe délivrant de la lumière blanche.
-
Décrire le phénomène obtenu. Que se passe-t'il quand
on translate le miroir
 parallèlement à
parallèlement à  ?
?
-
On dispose à la place de l'écran de la question 5-2 la fente
d'un spectroscope à prisme, disposée en
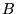 parallèlement à
parallèlement à 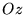 .
On déplace
.
On déplace  d'une distance
d'une distance 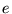 .
Qu'observe-t'on dans le spectroscope ? La lumière blanche utilisée
est supposée correspondre à des longueurs d'onde comprises
entre 400 et 750 nm ; décrire précisément le phénomène
si
.
Qu'observe-t'on dans le spectroscope ? La lumière blanche utilisée
est supposée correspondre à des longueurs d'onde comprises
entre 400 et 750 nm ; décrire précisément le phénomène
si
-
e=0.02 mm
-
e=1.5 mm
-
On revient au dispositif de la partie 2 : l'interféromètre
est réglé et l'onde incidente est monochromatique. On introduit
devant
 une lame à faces parallèles très mince d'indice
une lame à faces parallèles très mince d'indice  et d'épaisseur
et d'épaisseur 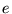 .
Que se passe-t'il ?
.
Que se passe-t'il ?
-
On effectue la même opération en lumière blanche
-
Que se passe-t'il lorsqu'on introduit la lame ? Comment et de combien doit-on
déplacer
 pour obtenir à nouveau des franges ?
pour obtenir à nouveau des franges ?
-
En fait l'indice du verre de la lame dépend de la longueur d'onde
suivant la loi
 .
Comment le résultat précédent est-il qualitativement
modifié ?
.
Comment le résultat précédent est-il qualitativement
modifié ?
-
Définir les trois termes : ordre zéro, frange achromatique,
teinte plate et les illustrer en utilisant les expériences décrites
dans cette question 6-4. Donner en particulier l'ordre
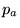 de la frange achromatique en fonction de
de la frange achromatique en fonction de 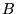 .
.
-
On règle un interféromètre de Michelson à la
teinte plate. Décrire succintement ce réglage. On introduit
ensuite devant le miroir
 la lame de verre utilisée précédemment. Que doit-on
faire pour retrouver la teinte plate ? Comparer avec le résultat
de la question 6-4.
la lame de verre utilisée précédemment. Que doit-on
faire pour retrouver la teinte plate ? Comparer avec le résultat
de la question 6-4.
-
Quelle est l'utilité de la lame compensatrice dans un interféromètre
réel ? Pourquoi a-t'on besoin de compenser le chemin optique parcouru
dans la lame séparatrice ?
7. Interféromètre
de Twyman
On reprend le dispositif de départ (partie 1), mais on rmplace le
miroir  par un miroir sphérique
par un miroir sphérique  (concave ou convexe) de rayon
(concave ou convexe) de rayon  =10
cm et d'axe
=10
cm et d'axe  .
On réalise
.
On réalise  .
.
-
L'observation se fait à l'oeil nu. Quel phénomène
d'interférences observe-t'on ? Déterminer la position des
franges brillantes. Le résultat est-il le même pour un miroir
convexe ou un miroir concave ?
-
On déplace
 dans le sens
dans le sens  .
Comment se déplacent les franges ?
.
Comment se déplacent les franges ?
-
Montrer comment un tel dispositif peut être utilisé pour détecter
les défauts de polissage d'une surface optique (lentille, prisme,...).
8. Mesures physiques faites à
l'aide du Michelson
Dans cette partie l'interféromètre est utilisé pour
réaliser des expériences mettant en jeu de faibles variations
d'indice. On l'utilise en ``coin d'air'' et on fait pour celà subir
au miroir  une rotation autour de
une rotation autour de 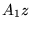 dans le sens trigonométrique, d'un angle
dans le sens trigonométrique, d'un angle  rad. La source est le laser+élargisseur de faisceau, et on projette
des franges verticales sur l'écran
rad. La source est le laser+élargisseur de faisceau, et on projette
des franges verticales sur l'écran 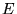 à l'aide d'une lentille (question 5-2). Le grandissement est
à l'aide d'une lentille (question 5-2). Le grandissement est  .
.
-
On produit, devant le miroir
 et parallèlement à celui-ci, un jet de butane horizontal
de diamètre 1 mm (typiquement le jet de gaz s'échappant d'un
briquet). L'indice de l'air dans les conditions de l'expérience
est de 1.00029, celui du butane de 1.00062. Donner, en la justifiant, l'allure
des franges obtenues.
et parallèlement à celui-ci, un jet de butane horizontal
de diamètre 1 mm (typiquement le jet de gaz s'échappant d'un
briquet). L'indice de l'air dans les conditions de l'expérience
est de 1.00029, celui du butane de 1.00062. Donner, en la justifiant, l'allure
des franges obtenues.
-
On place maintenant devant
 une cellule à faces parallèles d'épaisseur
une cellule à faces parallèles d'épaisseur 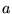 =1
cm qui contient initialement de l'air ambiant (
=1
cm qui contient initialement de l'air ambiant (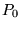 =1
bar,
=1
bar,  =293
K). On suppose que l'indice de réfraction
=293
K). On suppose que l'indice de réfraction  d'un gaz suit la loi de Gladstone :
d'un gaz suit la loi de Gladstone : 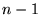 proportionnel à la masse volumique.
proportionnel à la masse volumique.
-
Montrer que si on comprime l'air de la cellule à température
constante, les franges se déplacent. Déterminer le sens du
déplacement et la surpression que l'on peut ainsi détecter
si l'on considère qu'on peut apprécier un déplacement
de frange de 0.05 interfrange. Les hypothèses utilisées seront
clairement indiquées.
-
Si l'air contenu dans la cellule est chauffé à la pression
constante de 1 bar, montrer que les franges se déplacent également.
Donner le sens du déplacement et la variation de température
que l'on peut détecter.
9. Interférences en lumière polarisée
Sur les bras d'un interféromètre réglé en coin
d'air et utilisé en lumière monochromatique de longueur d'onde  ,
on introduit, aux positions indiquées sur le dessin, des lames polarisantes
,
on introduit, aux positions indiquées sur le dessin, des lames polarisantes  ,
, 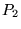 ,
,  ,
,  .
On appelle ``axe'' de la lame polarisante la direction du champ électrique
de l'onde qui en sort. On suppose que les éléments de l'interféromètre
(miroirs et séparatrice) n'influent pas sur la polarisation de la
lumière.
.
On appelle ``axe'' de la lame polarisante la direction du champ électrique
de l'onde qui en sort. On suppose que les éléments de l'interféromètre
(miroirs et séparatrice) n'influent pas sur la polarisation de la
lumière.

L'observation est faite dans la direction indiquée sur la figure
précédente, en notant  ,
, 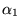 ,
, 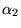 ,
,  les angles que font les axes des lames avec l'axe
les angles que font les axes des lames avec l'axe 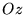 .
.
-
Au départ, on place seulement les polariseurs
 ,
, 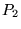 avec leurs axes parallèles à
avec leurs axes parallèles à 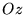 .
Que voit-on ?
.
Que voit-on ?
-
On fait tourner
 de
de  autour de
autour de  .
Que voit-on ? On conserve cette disposition des polariseurs croisés
dans la suite.
.
Que voit-on ? On conserve cette disposition des polariseurs croisés
dans la suite.
-
On ajoute la lame
 que l'on fait tourner autour de
que l'on fait tourner autour de 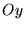 .
Calculer le contraste des franges en fonction de
.
Calculer le contraste des franges en fonction de  .
Pour quelles valeur de
.
Pour quelles valeur de  est-il maximal ?
est-il maximal ?
-
On retire
 et on introduit
et on introduit  .
Qu'observe-t'on pour une valeur donnée de
.
Qu'observe-t'on pour une valeur donnée de  ? Que se passe-t'il quand on fait tourner
? Que se passe-t'il quand on fait tourner  autour de
autour de  ?
?
-
On replace
 avec
avec  ,
en maintenant
,
en maintenant  .
Que se passe-t'il quand on fait tourner
.
Que se passe-t'il quand on fait tourner  autour de
autour de  ? Comparer à l'un des cas précédents.
? Comparer à l'un des cas précédents.
-
Qu'est-ce qu'une lame quart d'onde ? Qu'appelle-t-on axe rapide et axe
lent de la lame ?
-
 est enlevé ; on place le polariseur
est enlevé ; on place le polariseur  avec
avec  .
Devant
.
Devant  et
et  ,
on remplace les polariseurs par deux lames quart d'onde à la longueur
d'onde
,
on remplace les polariseurs par deux lames quart d'onde à la longueur
d'onde  ,
telles que
,
telles que 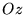 soit la bissectrice des angles entre axes lent et rapide des lames, bissectrice
intérieure pour l'une et bissectrice extérieure pour l'autre.
Que voit-on ? Justifier le résultat.
soit la bissectrice des angles entre axes lent et rapide des lames, bissectrice
intérieure pour l'une et bissectrice extérieure pour l'autre.
Que voit-on ? Justifier le résultat.
-
Le polariseur
 est toujours seul utilisé avec
est toujours seul utilisé avec  .
On place devant les miroirs
.
On place devant les miroirs  et
et  deux lames de quartz identiques et d'épaisseur 2.5 cm et de pouvoir
rotatoire 2170
deux lames de quartz identiques et d'épaisseur 2.5 cm et de pouvoir
rotatoire 2170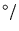 m.
Qu'est-ce que le pouvoir rotatoire ? Qu'obtient-on à la sortie ?
m.
Qu'est-ce que le pouvoir rotatoire ? Qu'obtient-on à la sortie ?
-
On garde le polariseur
 dans sa position précédente et on met sur les deux bras de
l'interféromètre deux cylindres de flint (verre au
plomb) de longueur 5 cm placés dans l'entrefer de deux électro-aimants
produisant un champ magnétique uniforme de 0.1 T parallèle
à la direction de propagation de la lumière, les deux champs
étant opposés (voir figure ci-après). La constante
de Verdet du flint, exprimant le pouvoir rotatoire par Telsa, est de 530
dans sa position précédente et on met sur les deux bras de
l'interféromètre deux cylindres de flint (verre au
plomb) de longueur 5 cm placés dans l'entrefer de deux électro-aimants
produisant un champ magnétique uniforme de 0.1 T parallèle
à la direction de propagation de la lumière, les deux champs
étant opposés (voir figure ci-après). La constante
de Verdet du flint, exprimant le pouvoir rotatoire par Telsa, est de 530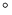 /m/T.
Qu'obtient-on dans la direction d'observation ? Quelle est la valeur numérique
du contraste des franges ?
/m/T.
Qu'obtient-on dans la direction d'observation ? Quelle est la valeur numérique
du contraste des franges ?

Footnotes
-
... Michelson1
-
Extrait de l'épreuve d'agrégation de physique, session de
2000 (durée de l'épreuve : 5 heures !)
![]() et on appelle axe du système la droite
et on appelle axe du système la droite ![]() normale à l'écran. On se place dans l'approximation de Gauss
(interférences en un point
normale à l'écran. On se place dans l'approximation de Gauss
(interférences en un point ![]() proche de l'axe).
proche de l'axe).

![]() et on appelle axe du système la droite
et on appelle axe du système la droite ![]() normale à l'écran. On se place dans l'approximation de Gauss
(interférences en un point
normale à l'écran. On se place dans l'approximation de Gauss
(interférences en un point ![]() proche de l'axe).
proche de l'axe).


![]() ,
, ![]() et
et ![]() de focales 5 mm, 20 cm et 1 m respectivement.
de focales 5 mm, 20 cm et 1 m respectivement.
![]() par
par ![]() .
Les deux largeurs
.
Les deux largeurs ![]() sont supposées identiques.
sont supposées identiques.

![]() ,
, ![]() ,
, ![]() ,
, ![]() les angles que font les axes des lames avec l'axe
les angles que font les axes des lames avec l'axe ![]() .
.
