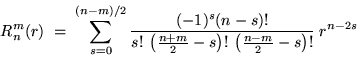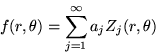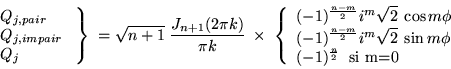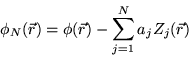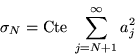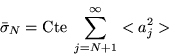Licence de Physique -- Devoir d'optique
Aberrations optiques
Pour le 26 Avril (Ste Alida)
Ce devoir vous paraitra peut-ètre difficile ; il vous permet
de confronter vos connaissances à un problème réel
(que vous pourriez rencontrer en travaillant dans un laboratoire d'optique
par exemple, ou sur des systèmes d'optique adaptative en astronomie).
Travaillez en physiciens : ce n'est pas un exercice de calcul.Interprétez
et commentez vos résultats, utilisez si vous le souhaitez l'outil
informatique pour faire les graphes, etc... il vaut mieux faire moins de
choses, mais les faire bien ! Nous vous conseillons de travailler en petits
groupes (4 maximum). Vous êtes libre de chercher des informations
complémentaires (fonctions de Bessel par exemple) partout où
vous voulez.
1. Aberrations et optique géométrique
-
Soit une onde d'amplitude complexe
![$A\; \exp i[\phi(x,y,z)-\omega t]$](img1.gif) .
Par un développement limité, montrer que cette onde peut
généralement ètre considérée comme localement
plane autour de tout point de coordonnées
.
Par un développement limité, montrer que cette onde peut
généralement ètre considérée comme localement
plane autour de tout point de coordonnées 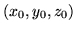 .
Ecrire le vecteur d'onde local en fonction de
.
Ecrire le vecteur d'onde local en fonction de 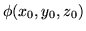 .
Citer des exemples où une telle approximation n'est pas possible.
.
Citer des exemples où une telle approximation n'est pas possible.
-
Soit une lentille mince convergente de focale
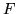 dans le vide, éclairée par une onde plane de longueur d'onde
dans le vide, éclairée par une onde plane de longueur d'onde 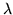 .
Ecrire dans l'approximation de Gauss l'équation des rayons lumineux
dans la sortie de la lentille (un rayon lumineux issu d'un point
.
Ecrire dans l'approximation de Gauss l'équation des rayons lumineux
dans la sortie de la lentille (un rayon lumineux issu d'un point 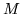 est une droite colinéaire au vecteur d'onde local en
est une droite colinéaire au vecteur d'onde local en 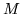 ).
Montrer que les rayons se croisent dans le plan focal image de la lentille.
).
Montrer que les rayons se croisent dans le plan focal image de la lentille.
-
On suppose maintenant que la lentille est asymétrique (défaut
de fabrication par exemple) ; dans la direction
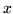 elle produit sur l'onde émergente un défaut de phase en
elle produit sur l'onde émergente un défaut de phase en 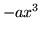 .
On travaille dans le plan
.
On travaille dans le plan 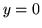 .
.
-
Etablir l'équation des rayons à la sortie de la lentille
-
Montrer que par un point
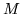 il passe 0 ou 2 rayons suivant que
il passe 0 ou 2 rayons suivant que 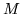 est d'un côté ou de l'autre d'une courbe appelée caustique
dont on déterminera l'équation près du foyer.
est d'un côté ou de l'autre d'une courbe appelée caustique
dont on déterminera l'équation près du foyer.
-
En un point
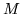 du côté éclairé de la caustique, montrer l'existence
de franges d'interférences dont on calculera l'interfrange.
du côté éclairé de la caustique, montrer l'existence
de franges d'interférences dont on calculera l'interfrange.
2. Un début de traitement
ondulatoire des aberrations
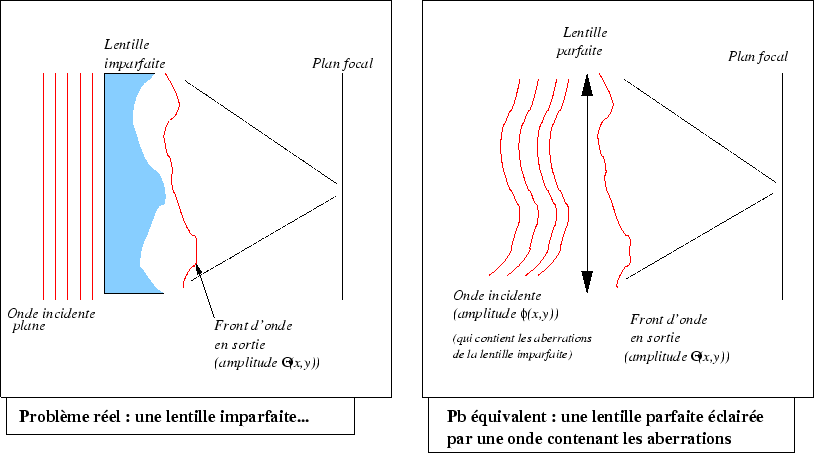
-
Soit une onde plane de vecteur d'onde
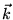 éclairant sous incidence normale une lentille convergente imparfaite
de coefficient de transmission
éclairant sous incidence normale une lentille convergente imparfaite
de coefficient de transmission 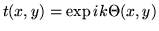 .
Montrer l'équivalence de ce problème avec celui d'une onde
non plane d'amplitude
.
Montrer l'équivalence de ce problème avec celui d'une onde
non plane d'amplitude 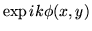 traversant une lentille convergente parfaite de focale
traversant une lentille convergente parfaite de focale 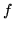 (phase quadratique en
(phase quadratique en 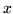 et
et 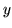 ).
Ecrire la relation entre
).
Ecrire la relation entre 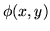 et
et 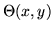 .
Que se passe-t'il au foyer quand
.
Que se passe-t'il au foyer quand 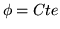 ? Peut-on dire à votre avis qu'il y a des aberrations dans ce cas
?
? Peut-on dire à votre avis qu'il y a des aberrations dans ce cas
?
-
Ecrire
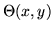 (sans approximation) dans le cas d'une lentille plan convexe d'indice
(sans approximation) dans le cas d'une lentille plan convexe d'indice 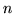 ,
de rayon de courbure
,
de rayon de courbure 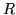 ,
de focale
,
de focale 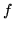 et de diamètre transversal
et de diamètre transversal 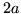 .
En déduire
.
En déduire 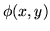 dans l'approximation au plus bas ordre non constant en
dans l'approximation au plus bas ordre non constant en 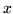 et
et 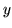 et faire le graphe de
et faire le graphe de 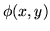 .
Quelle est la signification physique de cette fonction
.
Quelle est la signification physique de cette fonction 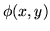 ?
?
-
On suppose que la lentille (supposée parfaitement mince pour cette
question : phase quadratique en
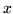 et
et 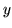 )
est limitée spatialement par un diaphragme de diamètre
)
est limitée spatialement par un diaphragme de diamètre 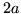 .
Ecrire l'amplitude au foyer de la lentille, préciser les dimensions
transversales de cette distribution d'amplitude.
.
Ecrire l'amplitude au foyer de la lentille, préciser les dimensions
transversales de cette distribution d'amplitude.
-
Défaut de mise au point : On
suppose que
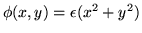 .
Quelle est la nature d'une telle onde ? Ecrire l'amplitude au foyer et
comparer au cas
.
Quelle est la nature d'une telle onde ? Ecrire l'amplitude au foyer et
comparer au cas 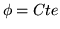 .
Montrer que l'onde converge en réalité dans un plan qui n'est
pas le plan focal de la lentille et commenter le titre donné à
ce parapgraphe.
.
Montrer que l'onde converge en réalité dans un plan qui n'est
pas le plan focal de la lentille et commenter le titre donné à
ce parapgraphe.
-
Aberration sphérique : Reprendre l'expression de
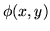 de la question 2. A quelles conditions a-t'on
de la question 2. A quelles conditions a-t'on 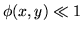 dans le disque de diamètre
dans le disque de diamètre 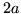 qui limite la lentille ? En approximant
qui limite la lentille ? En approximant 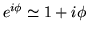 ,
calculer l'amplitude au foyer. Quelles différences par rapport au
cas
,
calculer l'amplitude au foyer. Quelles différences par rapport au
cas 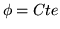 ? Même question pour l'intensité (un graphe de l'intensité
serait bienvenu à l'appui de la discussion).
? Même question pour l'intensité (un graphe de l'intensité
serait bienvenu à l'appui de la discussion).
3. Les modes de Zernike
3.1 Quelques définitions
La méthode traditionnellement utilisée pour traiter les aberrations
en optique ondulatoire consiste à développer la phase 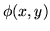 de l'onde sur une base de polynômes orthogonaux appelés modes
de Zernike. Ces modes sont définis en coordonnées polaires
sur un cercle de rayon unité et sont ainsi adaptés à
l'étude des fronts d'onde éclairant des optiques (lentilles,
diaphragmes) présentant la symétrie de révolution.
de l'onde sur une base de polynômes orthogonaux appelés modes
de Zernike. Ces modes sont définis en coordonnées polaires
sur un cercle de rayon unité et sont ainsi adaptés à
l'étude des fronts d'onde éclairant des optiques (lentilles,
diaphragmes) présentant la symétrie de révolution.
Ces modes sont définis par les relations :
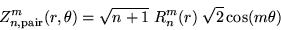
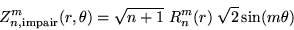
Il y a ainsi deux modes pour un couple 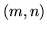 donné. Dans le cas où
donné. Dans le cas où 
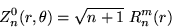
Les fonctions 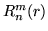 sont les polynômes de Zernike, définis pour
sont les polynômes de Zernike, définis pour 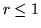 et s'écrivent
et s'écrivent
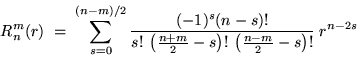
avec 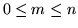 et
et 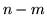 pair. Pour simplifier la manipulation de cette écriture un peu lourde,
les opticiens ont l'habitude d'une numérotation à un seul
indice
pair. Pour simplifier la manipulation de cette écriture un peu lourde,
les opticiens ont l'habitude d'une numérotation à un seul
indice 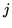 qui marche de la façon suivante :
qui marche de la façon suivante : 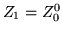 ,
, 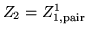 ,
, 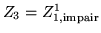 ,
, 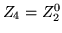 ,
etc...la parité de l'indice
,
etc...la parité de l'indice 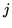 est celle de la dépendance en
est celle de la dépendance en 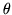 .
.
Voici un tableau résumant les 10 premiers modes de Zernike (plus
d'informations se trouvent sur le web, par exemple à l'adresse http://www.ctio.noao.edu/ atokovin/tutorial/index.html)
atokovin/tutorial/index.html)
| n |
m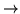 |
|
|
|
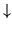 |
0 |
1 |
2 |
3 |
| 0 |
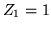 |
|
|
|
| 1 |
|
 |
|
|
| 1 |
|
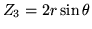 |
|
|
| 2 |
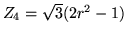 |
|
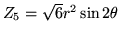 |
|
| 2 |
|
|
 |
|
| 3 |
|
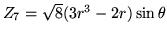 |
|
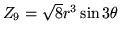 |
| 3 |
|
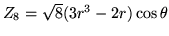 |
|
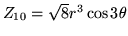 |
Ces modes forment une base orthonormée de fonctions par rapport
au produit scalaire suivant :
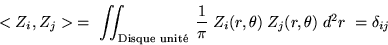
toute fonction 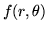 définie sur le disque de rayon unité se décompose
sur cette base de la façon suivante :
définie sur le disque de rayon unité se décompose
sur cette base de la façon suivante :
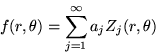
avec 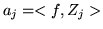 .
L'intérèt de cette base de fonctions est la séparation
des aberrations. Par exemple le terme
.
L'intérèt de cette base de fonctions est la séparation
des aberrations. Par exemple le terme 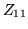 est l'aberration sphérique (en effet, une lentille parfaitement
stigmatique produit, en éclairage par une onde plane, des ondes
dont les fronts d'onde sont paraboliques et non sphériques), alors
que
est l'aberration sphérique (en effet, une lentille parfaitement
stigmatique produit, en éclairage par une onde plane, des ondes
dont les fronts d'onde sont paraboliques et non sphériques), alors
que 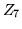 et
et 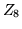 décrivent la coma (défaut observé en éclairage
très incliné).
décrivent la coma (défaut observé en éclairage
très incliné).
Les transformées de Fourier bidimensionnelles des modes de Zernike
sont données par :
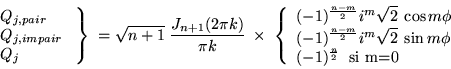
les fonctions 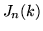 étant les fonctions de Bessel d'ordre
étant les fonctions de Bessel d'ordre 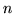 .
.
3.2 A vous maintenant !
-
Montrer l'orthogonalité (l'orthonormalité n'est pas demandée)
des modes non radiaux (
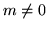 )
)
-
Une onde
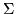 d'amplitude complexe
d'amplitude complexe 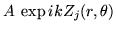 éclaire une lentille mince de diamètre transversal
éclaire une lentille mince de diamètre transversal 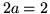 .
Ecrire et commenter l'intensité au foyer dans les cas suivants :
.
Ecrire et commenter l'intensité au foyer dans les cas suivants :
-
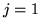 (terme dit ``de piston'')
(terme dit ``de piston'')
-
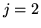 et
et 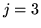 (termes de ``tip-tilt'')
(termes de ``tip-tilt'')
-
 (termes de ``défocalisation'') et comparer à la question
4 du paragraphe 2.
(termes de ``défocalisation'') et comparer à la question
4 du paragraphe 2.
-
Même question si l'amplitude complexe sur la pupille s'écrit
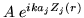 quel que soit
quel que soit 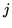 ,
mais en supposant
,
mais en supposant 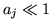 .
.
-
L'amplitude complexe de l'onde
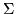 s'écrit maintenant
s'écrit maintenant  avec
avec  .
Montrer que la décomposition de la phase de
.
Montrer que la décomposition de la phase de 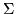 sur les modes de Zernike ne fait apparaitre que les termes radiaux (
sur les modes de Zernike ne fait apparaitre que les termes radiaux ( ).
Ecrire les premiers termes du développement (jusqu'à
).
Ecrire les premiers termes du développement (jusqu'à 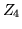 )
et en déduire l'intensité au foyer dans cette approximation.
Pousser le développement jusqu'au terme suivant et calculer l'intensité
au foyer. Dégagez l'influence sur l'image du dernier terme de Zernike
calculé (là encore, il est recommandé de produire
un graphe de l'intensité).
)
et en déduire l'intensité au foyer dans cette approximation.
Pousser le développement jusqu'au terme suivant et calculer l'intensité
au foyer. Dégagez l'influence sur l'image du dernier terme de Zernike
calculé (là encore, il est recommandé de produire
un graphe de l'intensité).
-
Reprendre l'expression de
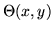 et de
et de 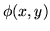 correspondant à la phase introduite par la traversée de la
lentille plan-convexe de la question 2 du §2 (l'éclairage est
toujours supposé sous incidence normale) On posera
correspondant à la phase introduite par la traversée de la
lentille plan-convexe de la question 2 du §2 (l'éclairage est
toujours supposé sous incidence normale) On posera 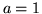 .
Montrer que la décomposition de
.
Montrer que la décomposition de 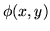 sur les modes de Zernike ne fait apparaitre que les termes radiaux (
sur les modes de Zernike ne fait apparaitre que les termes radiaux ( ).
Ecrire les premiers termes du développement (jusqu'à
).
Ecrire les premiers termes du développement (jusqu'à 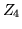 )
et en déduire l'intensité au foyer dans cette approximation.
)
et en déduire l'intensité au foyer dans cette approximation.
-
La lentille est légèrement astigmatique : les rayons de courbure
sont
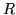 dans la direction
dans la direction 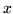 et
et 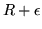 dans la direction
dans la direction 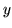 ,
avec
,
avec  .
L'éclairage est toujours sous incidence normale.
.
L'éclairage est toujours sous incidence normale.
-
Faire le développement sur les modes de Zernike jusqu'à
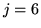 (les modes 5 et 6 correspondent à l'astigmatisme).
(les modes 5 et 6 correspondent à l'astigmatisme).
-
Ecrire les composantes du vecteur d'onde local à la sortie de la
lentille
-
Etablir l'équation des rayons à la sortie dans les plans
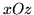 et
et 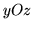
-
Faire un tracé des rayons dans chacun des plans. Que pensez-vous
de la focale de cette lentille ?
-
A quelle condition les termes d'aberration (termes non constants de
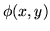 )
sont-ils faibles ? Dans cette approximation, calculer l'intensité
au foyer (on s'arrète au terme
)
sont-ils faibles ? Dans cette approximation, calculer l'intensité
au foyer (on s'arrète au terme 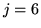 du développement de Zernike de
du développement de Zernike de 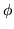 ).
Si possible, faites un graphe permettant la mise en évidence du
phénomène d'astigmatisme et commentez (comparer par exemple
à l'image produite par une lentille non astigmatique en faisant
tendre
).
Si possible, faites un graphe permettant la mise en évidence du
phénomène d'astigmatisme et commentez (comparer par exemple
à l'image produite par une lentille non astigmatique en faisant
tendre 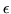 vers 0). Comparez à l'analyse géométrique de la question
précédente.
vers 0). Comparez à l'analyse géométrique de la question
précédente.
4. Optique adaptative
L'optique adaptative s'est développée dans la deuxième
moitié du XXe siècle, sur des motivations astrophysiques
: les télescopes butaient depuis le XVIIIe siècle sur les
déformations infligées aux images par la turbulence atmosphérique.
Des systèmes de correction en temps réel sont désormais
disponibles et sont basés sur une analyse en temps réel du
front d'onde perturbé couplée à un réseau de
petits pistons agissant sur un miroir souple pour rattraper les différences
de marche induites par la turbulence. Lors de l'anayse, la phase 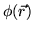 du font d'onde provenant d'une source ponctuelle (étoile non résolue,
l'onde serait plane en l'absence d'atmosphère) est décomposée
sur la base des modes de Zernike, fournissant ainsi un jeu de coefficients
du font d'onde provenant d'une source ponctuelle (étoile non résolue,
l'onde serait plane en l'absence d'atmosphère) est décomposée
sur la base des modes de Zernike, fournissant ainsi un jeu de coefficients 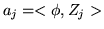 aléatoires. La décomposition est cependant infinie, et comme
d'habitude dans le cas de séries, on ne calcule qu'un nombre fini
de coefficients. La correction est alors partielle, elle se fait jusqu'à
un ordre
aléatoires. La décomposition est cependant infinie, et comme
d'habitude dans le cas de séries, on ne calcule qu'un nombre fini
de coefficients. La correction est alors partielle, elle se fait jusqu'à
un ordre 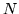 dépendant du système d'optique adaptative utilisé.
Après correction, l'onde possède une phase résiduelle
dépendant du système d'optique adaptative utilisé.
Après correction, l'onde possède une phase résiduelle
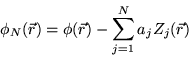
Ce sont les propriétés de la phase résiduelle
que nous vous proposons d'étudier dans cette partie du problème.
Dans toute la suite de ce paragraphe, on considère un système
optique composé d'une lentille mince convergente de rayon 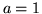 ,
éclairée par une onde d'amplitude
,
éclairée par une onde d'amplitude 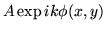 .
On définit l'erreur moyenne des fluctuations de la phase de l'onde
par leur écart-type
.
On définit l'erreur moyenne des fluctuations de la phase de l'onde
par leur écart-type 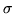 ,
défini par le rapport (les intégrales sont prises sur un
domaine correspondant à l'aire de la lentille)
,
défini par le rapport (les intégrales sont prises sur un
domaine correspondant à l'aire de la lentille)
![\begin{displaymath}\sigma^2=\frac{\int\!\!\!\int [\phi(\vec r)-\bar\phi]^2\; d^2r }{\pi}\end{displaymath}](img89.gif)
où 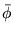 est la phase moyenne sur la lentille :
est la phase moyenne sur la lentille :
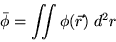
-
Un exemple simple pour commencer. L'onde incidente a une phase
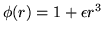 ,
le terme en
,
le terme en 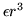 est à comprendre comme un écart à l'onde plane (un
défaut). Calculer les 3 premiers termes non nuls du développement
de Zernike, et en déduire
est à comprendre comme un écart à l'onde plane (un
défaut). Calculer les 3 premiers termes non nuls du développement
de Zernike, et en déduire 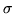 dans les cas suivants
dans les cas suivants
-
phase non corrigée
-
phase corrigée du premier terme non nul
-
phase corrigée des deux premiers termes non nuls
-
phase corrigée des trois premiers termes non nuls
Dans chaque cas, tracer le graphe de la phase, et discuter le gain apporté
par la correction partielle. On considère généralement
un front d'onde comme ``quasi-plan'' (c'est à dire donnant une image
de diffraction acceptable au foyer de la lentille) si l'écart-type
des fluctuations est inférieur à 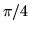 radians. Quelle est alors la valeur maximale de
radians. Quelle est alors la valeur maximale de 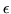 et de
et de 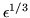 qui donne une erreur inférieure à
qui donne une erreur inférieure à 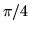 dans chacun des cas précédents. A votre avis, que représente
la variable
dans chacun des cas précédents. A votre avis, que représente
la variable 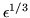 ?
?
-
Mêmes questions si la phase incidente s'écrit
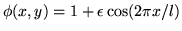 (cas d'une onde plane ayant subi une réflexion sur un plan d'eau
agité de vaguelettes). Réfléchissez sur la pertinence
de la décomposition de Zernike dans ce cas ; proposez éventuellement
une base plus adaptée pour développer
(cas d'une onde plane ayant subi une réflexion sur un plan d'eau
agité de vaguelettes). Réfléchissez sur la pertinence
de la décomposition de Zernike dans ce cas ; proposez éventuellement
une base plus adaptée pour développer 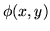 .
.
-
Soit
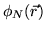 la phase d'une onde corrigée des
la phase d'une onde corrigée des 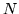 premiers modes de Zernike, et
premiers modes de Zernike, et 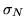 l'écart-type de ses fluctuations sur l'aire de la lentille. Montrer
que
l'écart-type de ses fluctuations sur l'aire de la lentille. Montrer
que
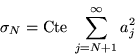
et déterminez la constante.
-
Dans le cas d'une phase aléatoire, comme celle introduite par la
turbulence atmosphérique, les
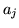 sont aléatoires, et l'on raisonne généralement sur
l'écart-type moyen (moyenné dans le temps) des fluctuations
de phase :
sont aléatoires, et l'on raisonne généralement sur
l'écart-type moyen (moyenné dans le temps) des fluctuations
de phase :
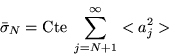
Pour l'atmosphère terrestre, 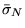 est donné par (Modèle de Fried, 1966)
est donné par (Modèle de Fried, 1966)
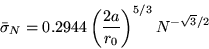
où 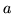 est le diamètre de l'optique utilisée et
est le diamètre de l'optique utilisée et 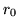 le paramètre dit de Fried qui caractérise l'état de
l'atmosphère (
le paramètre dit de Fried qui caractérise l'état de
l'atmosphère (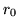 est le diamètre d'un télescope en dessous duquel les fluctuations
atmosphériques sont insensibles). En supposant
est le diamètre d'un télescope en dessous duquel les fluctuations
atmosphériques sont insensibles). En supposant  cm, Calculer le nombre
cm, Calculer le nombre 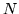 de modes à corriger pour obternir un défaut de phase inférieur
à
de modes à corriger pour obternir un défaut de phase inférieur
à 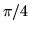 dans les cas suivants: (i)
dans les cas suivants: (i) 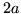 =10
cm, (ii)
=10
cm, (ii) 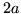 =1
m, (iii)
=1
m, (iii) 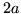 =8
m. Sachant qu'on arrive actuellement à corriger environ 300 modes,
quel est le diamètre
=8
m. Sachant qu'on arrive actuellement à corriger environ 300 modes,
quel est le diamètre 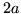 maximal utilisable ?
maximal utilisable ?
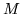 il passe 0 ou 2 rayons suivant que
il passe 0 ou 2 rayons suivant que 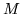 est d'un côté ou de l'autre d'une courbe appelée caustique
dont on déterminera l'équation près du foyer.
est d'un côté ou de l'autre d'une courbe appelée caustique
dont on déterminera l'équation près du foyer.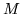 du côté éclairé de la caustique, montrer l'existence
de franges d'interférences dont on calculera l'interfrange.
du côté éclairé de la caustique, montrer l'existence
de franges d'interférences dont on calculera l'interfrange.