Soit
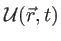 le champ électrique d'une onde quelconque. Ce champ est solution de l'équation
de propagation et est à ce titre une combinaison linéaire de fonctions de type
le champ électrique d'une onde quelconque. Ce champ est solution de l'équation
de propagation et est à ce titre une combinaison linéaire de fonctions de type
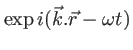 .
Si l'onde est monochromatique, la pulsation est la même pour tous les termes de la combinaison
linéaire et il vient en facteur un
.
Si l'onde est monochromatique, la pulsation est la même pour tous les termes de la combinaison
linéaire et il vient en facteur un
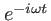 . Le champ s'écrit alors :
. Le champ s'écrit alors :
la partie spatiale
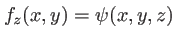 est simplement l'amplitude complexe de l'onde
est simplement l'amplitude complexe de l'onde
Soit 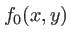 l'amplitude supposée connue d'une onde monochromatique quelconque dans le
plan
l'amplitude supposée connue d'une onde monochromatique quelconque dans le
plan 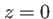 . Cette fonction bidimensionnelle est somme de sa transformée de Fourier :
. Cette fonction bidimensionnelle est somme de sa transformée de Fourier :
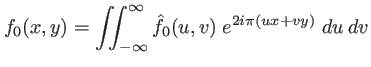 |
(1.16) |
Faisons le changement de variables
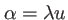 ,
,
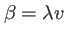 où
où 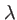 est la
longueur d'onde. Il vient
est la
longueur d'onde. Il vient
![$\displaystyle f_0(x,y)=\int\!\!\!\int \frac{1}{\lambda^2}\; \hat{f}_0\left(\fra...
... \exp\left[\frac{2i\pi}{\lambda} (\alpha x+\beta y)\right] \; d\alpha \: d\beta$](img211.png) |
(1.17) |
La quantité
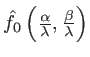 est appelée spectre angulaire de
est appelée spectre angulaire de 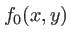 . Comparons cette expression à l'équation 1.14 exprimant une somme discrète d'ondes planes dans le
plan
. Comparons cette expression à l'équation 1.14 exprimant une somme discrète d'ondes planes dans le
plan 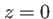 . Nous avons ici la même formule en ayant remplacé la somme discrète par une
intégrale. L'amplitude
. Nous avons ici la même formule en ayant remplacé la somme discrète par une
intégrale. L'amplitude 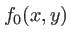 apparait alors comme une somme continue d'ondes planes se
propageant dans des directions
apparait alors comme une somme continue d'ondes planes se
propageant dans des directions
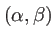 . Le terme
. Le terme
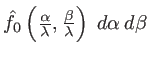 est
l'équivalent du
est
l'équivalent du 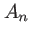 de la formule 1.14 et représente le poids de
chacune des ondes planes dans la somme. Pour obtenir l'expression
de la formule 1.14 et représente le poids de
chacune des ondes planes dans la somme. Pour obtenir l'expression 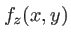 de l'amplitude de l'onde
dans un plan
de l'amplitude de l'onde
dans un plan 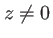 il suffit de multiplier chaque onde plane par un terme
il suffit de multiplier chaque onde plane par un terme
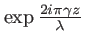 où
où
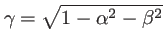 , puis de faire la somme. Il vient :
, puis de faire la somme. Il vient :
![$\displaystyle f_z(x,y)=\int\!\!\!\int \frac{1}{\lambda^2}\; \hat{f}_0\left(\fra...
...t[\frac{2i\pi}{\lambda} (\alpha x+\beta y+\gamma z)\right] \; d\alpha \: d\beta$](img220.png) |
(1.18) |
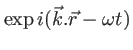 .
Si l'onde est monochromatique, la pulsation est la même pour tous les termes de la combinaison
linéaire et il vient en facteur un
.
Si l'onde est monochromatique, la pulsation est la même pour tous les termes de la combinaison
linéaire et il vient en facteur un
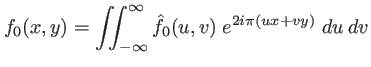
![$\displaystyle f_0(x,y)=\int\!\!\!\int \frac{1}{\lambda^2}\; \hat{f}_0\left(\fra...
... \exp\left[\frac{2i\pi}{\lambda} (\alpha x+\beta y)\right] \; d\alpha \: d\beta$](img211.png)
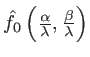 est appelée spectre angulaire de
est appelée spectre angulaire de 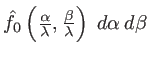 est
l'équivalent du
est
l'équivalent du ![$\displaystyle f_z(x,y)=\int\!\!\!\int \frac{1}{\lambda^2}\; \hat{f}_0\left(\fra...
...t[\frac{2i\pi}{\lambda} (\alpha x+\beta y+\gamma z)\right] \; d\alpha \: d\beta$](img220.png)