Principe de Huygens-Fresnel

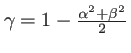On se place pour la suite du raisonnement dans les conditions de l'optique paraxiale. Posant $\gamma=1-\frac{\alpha^2+\beta^2}{2}$ , l'expression de $f_z(x,y)$ devient^(*)

$$f_z(x,y)=e^\frac{2 i \pi z}{\lambda} \; \int\!\!\!\int \frac{1}{\... ... \exp\left[\frac{2i\pi}{\lambda} (\alpha x+\beta y)\right] \; d\alpha \: d\beta$$ (1.19)

le changement de variable $u=\alpha/\lambda$ , $v=\beta/\lambda$ donne

$$f_z(x,y)=e^\frac{2 i \pi z}{\lambda} \; \int\!\!\!\int \hat{f}_0(... ...; \exp\left[-i\pi \lambda z (u^2+v^2)\right] \; e^{2i\pi (u x+v y)} \; du \: dv$$ (1.20)

et en posant

$$\hat{g}_0(u,v)=\exp\left[-i\pi \lambda z (u^2+v^2)\right]$$

on cette expression est celle d'une transformée inverse de Fourier :

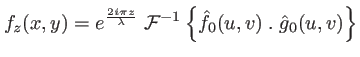$$f_z(x,y)=e^\frac{2 i \pi z}{\lambda} \; {\cal F}^{-1}\left\{\hat{f}_0(u,v) \; .\; \hat{g}_0(u,v)\right\}$$ (1.21)

dans laquelle ${\cal F}$ désigne la transformée de Fourier (T.F.). Il vient

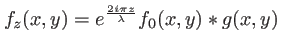$$f_z(x,y)=e^\frac{2 i \pi z}{\lambda} f_0(x,y) \ast g(x,y)$$ (1.22)

la fonction $g(x,y)$ peut se calculer avec les relations entre T.F. suivantes :

$$\begin{array}{l} \displaystyle {\cal F}\left\{e^{i\pi x^2}\r... ...c{1}{\vert a\vert} \hat h\left({\frac{u}{a}}\right) \end{array}$$

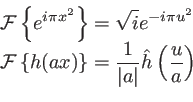
La deuxième de ces relations n'est valable qu'à la condition $\arg (a)<\pi/4$ et n'est en particulier pas valable quand $a=i$ (les résultats connus sur les TF de gaussiennes ne s'appliquent pas pour trouver la TF de $e^{i\pi x^2}$ qui soit faire l'objet d'un calcul spécifique par exemple par la méthode des résidus). Il vient

$$g(x,y)=\frac{1}{i\lambda z} \exp \left[i\pi\frac{x^2+y^2}{\lambda z}\right]$$ (1.23)

et la transformée de Fresnel s'écrit comme une convolution

$$\mbox{\fbox{$\displaystyle f_z(x,y)=e^\frac{2 i \pi z}{\lambda} f... ...) \ast \frac{1}{i\lambda z} \exp\left[ i\pi\frac{x^2+y^2}{\lambda z}\right] $}}$$ (1.24)

la fonction $g(x,y)$ est la réponse impulsionnelle de la diffraction de Fresnel. Cette dernière peut ainsi être interprétée comme un filtrage linéaire des fréquences spatiales de $f_0$ .
En remarquant que le terme

$$\frac{1}{z} e^\frac{2 i \pi z}{\lambda} \exp \left[i\pi\frac{x^2+y^2}{\lambda z}\right]$$

est l'expression d'une onde sphérique en optique paraxiale, on peut mettre $f_z$ sous la forme plus générale :

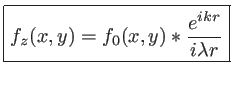$$\mbox{\fbox{$\displaystyle f_z(x,y)= f_0(x,y) \ast \frac{e^{ikr}}{i\lambda r} $}}$$ (1.25)

avec $r=\sqrt{x^2+y^2+z^2}$ , la convolution portant uniquement sur les variables $x$ et $y$ .

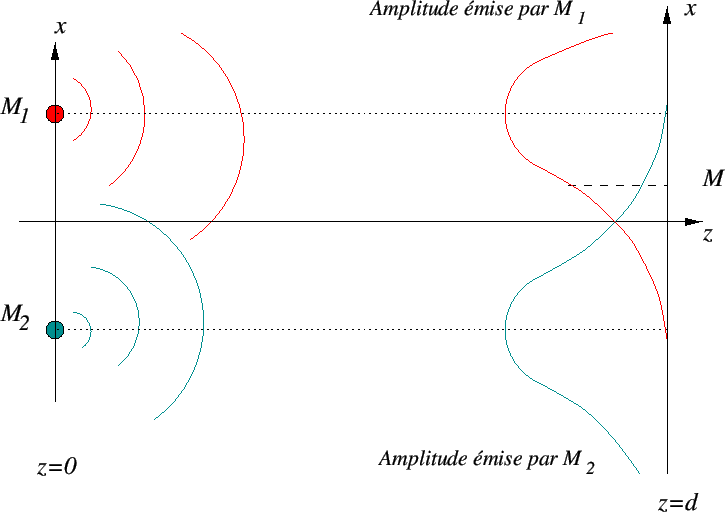
Ce résultat est connu sous le nom de Principe de Huygens-Fresnel. Il peut s'interpréter de la manière suivante : chaque point du plan $z=0$ émet une onde sphérique d'amplitude proportionnelle à $f_0(x,y)$ . Toutes ces ondes sphériques se propagent et l'amplitude en un point du plan $z$ est la somme des amplitudes de toutes ces ondes sphériques. La figure 1.4 illustre ce phénomène.

Fig. 1.4: Illustration du principe de Huygens-Fresnel. L'onde dans le plan $z=0$ est découpée en une infinité de points-source comme les points $M_1$ et $M_2$ sur le dessin. Ces points-sources émettent chacun une onde sphérique dans la direction $z>0$ . L'amplitude de ces ondes sphériques est proportionnelle à la valeur de l'amplitude de l'onde incidente au niveau des points-sources. En un point $M$ du plan $z=d$ , les amplitudes des ondes sphériques émises par chacun des poins s'ajoutent. L'amplitude en $M$ est la somme de toutes ces amplitudes.

Les simulations ci-apr?s présentent l'évolution d'une onde issue d'un objet constitué de points-source (f0(x,y) est alors une somme de Delta de Dirac). L'onde dans le plan z=0 se propage de plan z=Cte en plan z=Cte en se déformant. On représente l'intensité telle qu'elle serait vue par une caméra placée dans chacun de ces plans, comme schématisé ci-dessous :



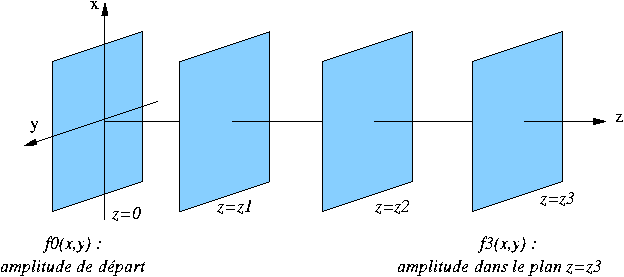
La longueur d'onde choisie est de 1 mm, la distance entre les points-source est de l'ordre de 1 a 3 mm. 3 simulations sont présentées : 1 point-source, 2 points-source et 4 points-source. Sur ces deux derni?res, des franges d'interférences sont visibles dans le recouvrement des ondes sphériques émises par les différents point-sources. A grande distance dans le cas des deux sources, on retrouve les franges d'Young.




On trouvera d'autes simulations sur le site http://daugerresearch.com/fresnel.

Une partie de ce principe a été énoncée par Huygens en 1678 : chaque partie de la surface d'onde se comporte comme une source secondaire émettant une quantité de lumière proportionnelle à celle reçue par la source secondaire. Il a été complété par Fresnel en 1818 avec l'idée d'addition cohérente en chaque point des amplitudes des ondes émises par chaque source secondaire. Le nom de ``principe de Huygens-Fresnel'' date de 1818.

On doit la première démonstration mathématique à Kirchhoff (1882), sous certaines hypothèses : longueurs d'ondes grandes devant les distances inter-atomiques, matériaux constituants les éléments optiques ``inertes" : par exemple un diaphragme en acier produit les mêmes effets qu'un diaphragme en plastique. En 1896, Sommerfeld a réalisé un traitement électromagnétique complet du problème de la diffraction d'une onde plane qui rencontre un demi-plan infini parfaitement conducteur.

Il est à noter que le principe de Huygens-Fresnel, établi ici en optique paraxiale, reste valable quelle que soit l'incidence. Des démonstrations mathématiques existent qui font intervenir les fonctions de Green (voir par exemple le Born et Wolf, ``Principle of Optics'').

Note : ^(*)

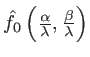Le lecteur aura remarqué que l'approximation paraxiale est faite alors que l'intégration va de $-\infty$ à $\infty$ pour les variables $\alpha$ et $\beta$ . Cette approximation n'est en fait possible que si la fonction $\hat{f}_0\left(\frac{\alpha}{\lambda},\frac{\beta}{\lambda}\right)$ est rapidement décroissante de manière à limiter le domaine où l'intégrale a des valeurs significatives (support 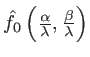$\ll 1$ ). Si la fonction $f_0(x,y)$ a un support $a$ (cas d'une one plane ayant traversé un diaphragme de diamètre $a$ ), alors $\hat{f}_0\left(\frac{\alpha}{\lambda},\frac{\beta}{\lambda}\right)$ a un support $\frac{\lambda}{a}$ . La condition sur le support de $\hat{f}_0$ impose donc la condition $a\gg \lambda$  : la diffraction de Fresnel telle que nous la décrivons est valable si les éléments optiques rencontrées par l'onde ont une taille grande devant la longueur d'onde. Dans le domaine des rayons X, les distances inter-atomiques sont comparables à $\lambda$ et l'on utilise la diffraction de Bragg.