Transformée de Fourier-Fresnel

En optique paraxiale on peut mettre l'équation 1.24 sous une forme un peu différente plus pratique pour certains calculs. On explicite le produit de convolution :

$$f_z(x,y)=\frac{e^{ikz}}{i\lambda z} \; \int\!\!\!\int f_0(x',y') ... ...xp\left[\frac{i\pi}{\lambda z}\left((x-x')^2+(y-y')^2\right)\right]\; dx'\: dy'$$ (1.26)

et on fait apparaitre l'expression d'une TF à deux dimensions :

$$f_z(x,y)=\frac{e^{ikz}}{i\lambda z} \; \exp\left[\frac{i\pi}{\lam... ...'^2+y'^2) \right]\; \exp\left[\frac{2i\pi}{\lambda z}(x x'+y y')\right] dx' dy'$$ (1.27)

que l'on peut écrire à l'aide de la notation ${\cal F}_{u,v} \{f(x,y)\} = \hat{f}(u,v)$  :

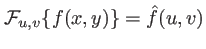$$\mbox{\fbox{$\displaystyle f_z(x,y)=\frac{e^{ikz}}{i\lambda z} \;... ...ft\{ f_0(x',y') \exp\left[\frac{i\pi}{\lambda z}(x'^2+y'^2)\right] \right\} $}}$$ (1.28)

cette relation est la transformée de Fourier-Fresnel.