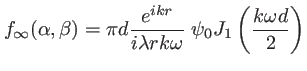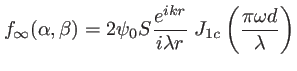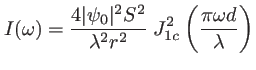Soit un trou de diamètre 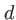 éclairé sous incidence normale par une onde plane d'amplitude
éclairé sous incidence normale par une onde plane d'amplitude 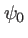 dans le plan
dans le plan 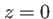 . L'écran et l'onde incidente sont à symétrie de révolution autour de l'axe optique, la figure de diffraction sera donc aussi à symétrie de révolution.
. L'écran et l'onde incidente sont à symétrie de révolution autour de l'axe optique, la figure de diffraction sera donc aussi à symétrie de révolution.
Posons
-
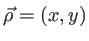 les coordonnées cartésiennes d'un point dans le plan du trou
les coordonnées cartésiennes d'un point dans le plan du trou
-
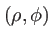 les coordonnées polaires correspondantes
les coordonnées polaires correspondantes
-
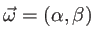 les deux premières composantes d'un vecteur unitaire indiquant une direction dans le plan
les deux premières composantes d'un vecteur unitaire indiquant une direction dans le plan 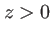
-
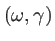 les coordonnées polaires correspondantes
les coordonnées polaires correspondantes
L'amplitude diffractée dans la direction
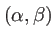 s'écrit
s'écrit
avec ici
donc
ou encore
passage en polaires :
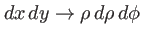 ,
,
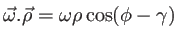 et en posant
et en posant
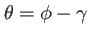 , il vient
, il vient
Introduisons maintenant la fonction de Bessel
il vient
La relation suivante entre les fonctions de Bessel 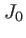 et
et 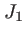
nous permet d'écrire
soit en introduisant la fonction ``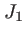 cardinal''
cardinal''
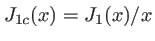
L'intensité s'écrit
Fig;. 1.14:
Figure de diffraction d'un trou circulaire. L'intensité diffractée est décrite par une fonction 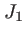 cardinal carré à symétrie de révolution autour de l'axe optique (voir le texte). (a) Trou ; (b) Figure de diffraction (intensité) ; (c) Figure de diffraction d'un trou plus petit ; (d) Graphe de la fonction
cardinal carré à symétrie de révolution autour de l'axe optique (voir le texte). (a) Trou ; (b) Figure de diffraction (intensité) ; (c) Figure de diffraction d'un trou plus petit ; (d) Graphe de la fonction
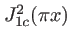 ; (e) Zoom de la courbe (d).
; (e) Zoom de la courbe (d).
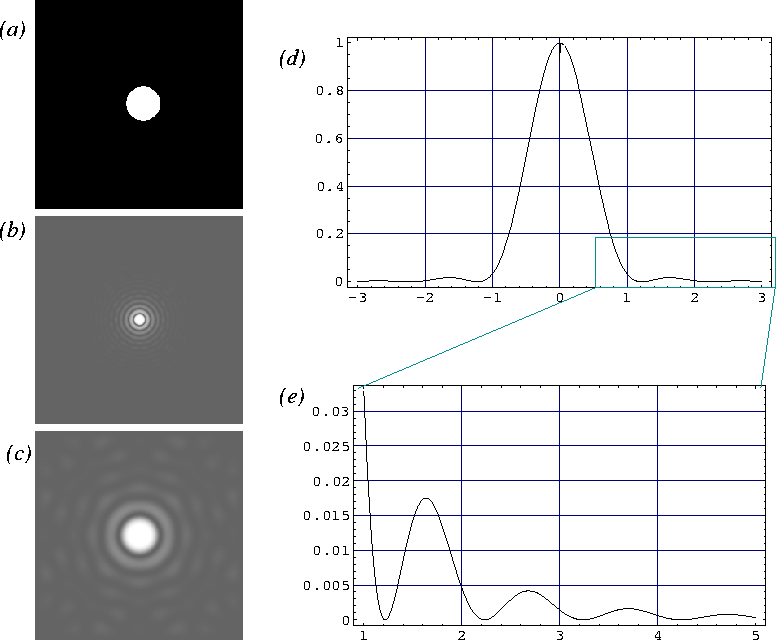
|
avec
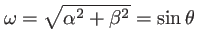 ,
, 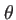 étant l'angle des coordonnées cylindriques défini au paragraphe 1.1.1. On remarque comme on s'y attendait que l'intensité est à symétrie de révolution autour de
étant l'angle des coordonnées cylindriques défini au paragraphe 1.1.1. On remarque comme on s'y attendait que l'intensité est à symétrie de révolution autour de 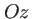 . Cette fonction appelée ``fonction d'Airy'' est maximum au centre et présente un comportement oscillatoire : la figure bidimensionnelle est une tache brillante entourée d'anneaux noirs et brillants comme on peut le voir sur la figure 1.14. Les rayons angulaires des premiers anneaux et la valeur de l'intensité sur les anneaux brillants sont donnés dans le tableau suivant :
. Cette fonction appelée ``fonction d'Airy'' est maximum au centre et présente un comportement oscillatoire : la figure bidimensionnelle est une tache brillante entourée d'anneaux noirs et brillants comme on peut le voir sur la figure 1.14. Les rayons angulaires des premiers anneaux et la valeur de l'intensité sur les anneaux brillants sont donnés dans le tableau suivant :
| |
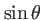
|
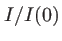
|
| 1er anneau noir |
1.22 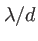
|
0 |
| 1er anneau brillant |
1.63 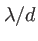
|
0.017 |
| 2e anneau noir |
2.23 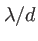
|
0 |
| 2e anneau brillant |
2.68 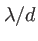
|
0.004 |
| 3e anneau noir |
3.23 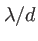
|
0 |
| 3e anneau brillant |
3.70 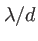
|
0.0016 |
La fraction de l'intensité diffractée dans le pic central sur l'intensité diffractée dans tout l'espace est ici de 83.8 % (à comparer à 81.5 % pour une ouverture carrée de côté 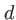 ).
).
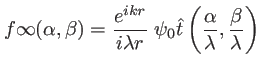
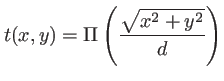

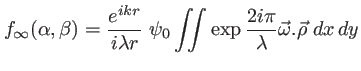
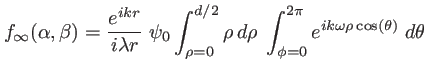
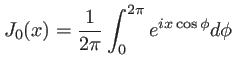
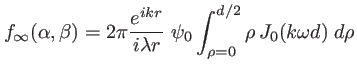
![$\displaystyle x J_0(x)=\frac{d}{dx} [x J_1(x)]
$](img417.png)