L3 Physique -- Examen d'optique
Session 1 -- 28 Avril 2015
Durée 3h. Documents autorisés : une feuille A4 recto-verso manuscrite, formulaire de TF.
Lisez bien tous les mots et toutes les lettres de l'énoncé. Car une réponse qui est seulement ``presque juste'' est aussi ``tout à fait fausse''...
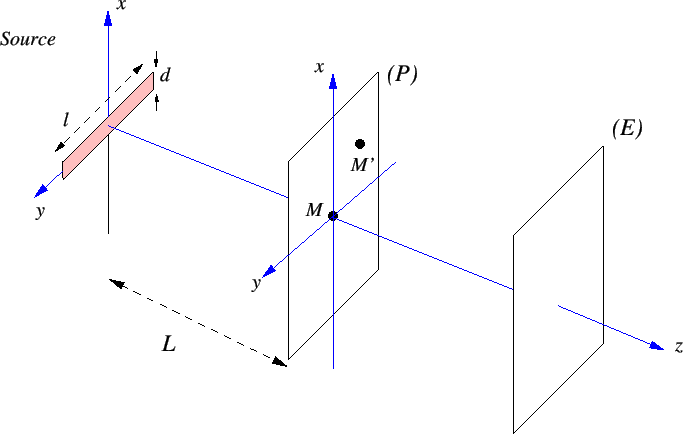
Un filament d'ampoule spatialement incohérent est assimilable à une source plate, rectangulaire de largeurs 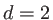 mm dans la direction
mm dans la direction 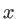 , et
, et 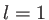 cm dans la direction
cm dans la direction 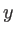 , éclaire un écran
, éclaire un écran 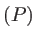 situé à une distance
situé à une distance 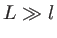 . La source est supposée monochromatique de longueur d'onde
. La source est supposée monochromatique de longueur d'onde 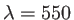 nm. Un expérimentateur perce l'écran
nm. Un expérimentateur perce l'écran 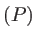 de deux trous quasi-ponctuels, en deux points
de deux trous quasi-ponctuels, en deux points 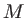 de coordonnées
de coordonnées 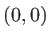 et
et 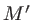 de coordonnées
de coordonnées 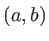 dans le but de réaliser une expérience d'interférences.
dans le but de réaliser une expérience d'interférences.
- Dans quelle direction doit-il placer le trou
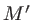 pour avoir le plus de chances d'observer des interférences, et pourquoi ? Dans la suite, on suppose cette condition réalisée.
pour avoir le plus de chances d'observer des interférences, et pourquoi ? Dans la suite, on suppose cette condition réalisée.
- Ecrire la distribution angulaire de brillance du filament vu depuis le plan
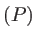 . En déduire son degré de cohérence spatiale.
. En déduire son degré de cohérence spatiale.
- A quelle distance
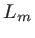 de
de 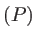 l'expérimentateur doit-il placer le filament pour que les points
l'expérimentateur doit-il placer le filament pour que les points 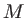 et
et 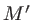 soient suffisamment cohérents entre eux (degré de cohérence
soient suffisamment cohérents entre eux (degré de cohérence 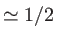 ) ? On donne ci-après une table de valeurs de la fonction sinc.
) ? On donne ci-après une table de valeurs de la fonction sinc.
- On réalise
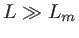 . Les franges produites par les points
. Les franges produites par les points 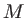 et
et 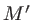 sont observées sur dans le plan
sont observées sur dans le plan 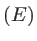 situé à une distance
situé à une distance 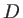 de
de 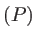 . Quel sera le contraste des franges ?
. Quel sera le contraste des franges ?
- Même question si
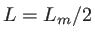 .
.
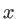 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
2 |
2.2 |
2.4 |
2.6 |
2.8 |
sinc 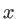 |
1 |
0.99 |
0.97 |
0.94 |
0.89 |
0.84 |
0.78 |
0.70 |
0.62 |
0.54 |
0.45 |
0.37 |
0.28 |
0.20 |
0.12 |
Une onde plane monochromatique de longueur d'onde 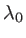 et d'amplitude
et d'amplitude 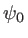 éclaire sous incidence normale un biprisme formé de deux prismes identiques d'indice
éclaire sous incidence normale un biprisme formé de deux prismes identiques d'indice 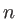 et d'angle faible
et d'angle faible 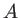 (voir schéma ci-contre). L'épaisseur maximale des prismes est notée
(voir schéma ci-contre). L'épaisseur maximale des prismes est notée 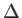 . Les prismes sont supposés de dimensions supposées infinies dans la direction
. Les prismes sont supposés de dimensions supposées infinies dans la direction 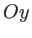 . Ce biprisme est placé dans le plan
. Ce biprisme est placé dans le plan 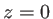 , on observe dans le plan
, on observe dans le plan 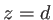 . Dans tout le problème, on néglige la diffraction par les bords des prismes, ce qui revient à considérer que les ondes 1 et 2 en sortie de chaque prisme sont planes. On donne les valeurs numériques suivantes :
. Dans tout le problème, on néglige la diffraction par les bords des prismes, ce qui revient à considérer que les ondes 1 et 2 en sortie de chaque prisme sont planes. On donne les valeurs numériques suivantes : 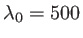 nm,
nm, 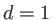 m,
m, 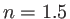 ,
, 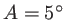 .
.
![\includegraphics[width=7cm]{biprism1.eps}](img48.png)
- Ecrire, dans l'approximation paraxiale, le coefficient de transmission du prisme 1 (négliger les effets de bords : on ne multipliera pas par une porte qui limite la taille du prisme). En déduire l'expression de l'onde 1 dans le plan
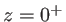 à la sortie du prisme, puis dans le plan
à la sortie du prisme, puis dans le plan 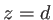 .
.
- Mêmes questions pour le prisme 2 et l'onde 2.
- Calculer l'intensité
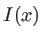 dans le plan
dans le plan 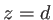 , donner l'interfrange
, donner l'interfrange 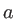 .
.
NB : il est possible de passer à la question 7 (paragraphe 2.2) sans traiter les questions 4 à 6.
- Montrer que l'intensité peut se mettre sous la forme
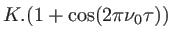 avec
avec 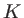 une constante,
une constante, 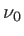 la fréquence associée à
la fréquence associée à 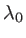 et
et 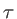 une variable dont on précisera l'expression en fonction de
une variable dont on précisera l'expression en fonction de 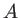 et
et 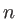 . Quelle est la signification physique de
. Quelle est la signification physique de 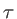 ?
?
- L'onde incidente, toujours plane et sous incidence normale, est cette fois quasi-monochromatique autour de la longueur
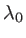 , avec un profil spectral
, avec un profil spectral 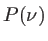 ,
, 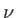 étant la fréquence. Ecrire l'intensité des franges dans ce cas.
étant la fréquence. Ecrire l'intensité des franges dans ce cas.
- L'observation révèle des franges dont le contraste décroit avec la distance au centre, comme sur la figure ci-dessous. La fonction contraste montre un comportement de la forme
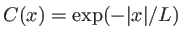 avec
avec 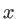 la distance et
la distance et 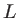 une largeur caractéristique. Cette fonction est tracée sur le graphe de droite, en fonction de la variable
une largeur caractéristique. Cette fonction est tracée sur le graphe de droite, en fonction de la variable  .
.
![\includegraphics[width=19cm]{frprism.eps}](img49.png)
- Question indépendante : Comment a-t-on pu faire pour mesurer le contraste local
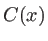 à partir de l'intensité des franges ?
à partir de l'intensité des franges ?
- Soit
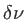 la largeur spectrale de la fonction profil. Donner la définition et l'expression du temps
la largeur spectrale de la fonction profil. Donner la définition et l'expression du temps 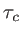 de cohérence temporelle de l'onde. En déduire une relation entre
de cohérence temporelle de l'onde. En déduire une relation entre 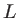 et
et 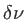 . A.N. calculer
. A.N. calculer
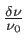 avec les données numériques de l'énoncé et
avec les données numériques de l'énoncé et 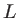 mesuré sur le graphe (on ne demande pas une grande précision).
mesuré sur le graphe (on ne demande pas une grande précision).
- En déduire un ordre de grandeur de la longueur de cohérence temporelle de cette onde.
- Exprimer le contraste en fonction de
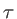 , puis calculer, à une constante multiplicatice près, le spectre
, puis calculer, à une constante multiplicatice près, le spectre 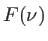 de la lumière incidente en fonction de la fréquence
de la lumière incidente en fonction de la fréquence 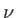 . A quel forme de profil a-t-on affaire ?
. A quel forme de profil a-t-on affaire ?
Le biprisme est cette fois forme de deux prismes anisotropes uniaxe taillés dans le même cristal, mais dont les axes optiques sont orientés comme sur le schéma ci-contre : axe parallèle à 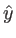 pour le prisme 1, axe parallèle à
pour le prisme 1, axe parallèle à 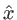 pour le prisme 2. Les indices ordinaire et extraordinaire sont notés respectivement
pour le prisme 2. Les indices ordinaire et extraordinaire sont notés respectivement 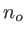 et
et 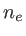 . Comme précédemment, l'angle au sommet des deux prismes est
. Comme précédemment, l'angle au sommet des deux prismes est 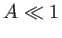 et l'épaisseur maximale est
et l'épaisseur maximale est 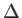 . L'ensemble toujours supposé de dimensions infinies dans la direction
. L'ensemble toujours supposé de dimensions infinies dans la direction 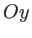 .
.
L'éclairage est fait sous incidence normale par une onde plane monochromatique de longueur d'onde 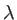 et d'amplitude
et d'amplitude 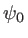 Ce biprisme est placé dans le plan
Ce biprisme est placé dans le plan 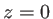 , on observe dans le plan
, on observe dans le plan 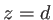 . Là encore, on négligera la diffraction par les bords des prismes.
. Là encore, on négligera la diffraction par les bords des prismes.
![\includegraphics[width=7cm]{biprism2.eps}](img62.png) 6
6
- Le champ incident a une polarisation rectiligne parallèle à
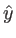 .
.
- Quel est l'état de polarisation de l'onde 1 à la sortie du prisme 1 ?
- Ecrire le coefficient de transmission associé au prisme 1
- Ecrire le champ électrique
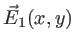 de l'onde 1 dans le plan
de l'onde 1 dans le plan 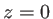 puis dans le plan
puis dans le plan 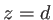 (se limiter à une approximation à l'ordre 1 en
(se limiter à une approximation à l'ordre 1 en 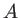 ).
).
- Mêmes questions pour le prisme 2 et l'onde 2
- Ecrire l'intensité des franges dans le plan
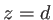 . Préciser l'interfrange
. Préciser l'interfrange 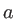 et la position
et la position 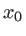 du centre des franges.
du centre des franges.
- Rappeler la définition de la biréfringence du cristal. Intervient-elle dans ce problème ?
- Le champ incident a une polarisation rectiligne parallèle à
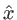 . Comment est modifiée l'intensité des franges ?
. Comment est modifiée l'intensité des franges ?
- Le champ incident a une polarisation rectiligne qui fait un angle de
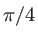 avec l'axe
avec l'axe 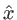
- Préciser l'orientation des lignes neutres des prismes et écrire le vecteur de Jones du champ incident dans cette base.
- Expliquer pourquoi on observe 4 ondes planes de type
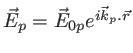 à la sortie du biprisme. Préciser leur amplitude
à la sortie du biprisme. Préciser leur amplitude 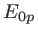 , leur direction de polarisation et leur vecteur d'onde
, leur direction de polarisation et leur vecteur d'onde 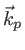 .
.
- Parmi ces 4 ondes, préciser celles qui sont cohérentes entre elles et celles qui ne le sont pas.
- Proposer une méthode pour calculer l'intensité dans le plan
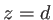 . Le calcul lui-même n'est pas demandé.
. Le calcul lui-même n'est pas demandé.
- Rappeler la définition du pouvoir de résolution d'un réseau au sens de Rayleigh. Un réseau par transmission est gravé sur un support carré de côté 1cm, il possède 100 périodes par mm. Quel est son pouvoir de résolution dans l'ordre -2 ? Combien voit-on d'ordres diffractés à la longueur d'onde
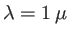 m?
m?
- Décrire en quelques lignes le phénomènes d'interférences localisées en faisant ressortir notamment la différence avec des interférences non localisées. Citer un exemple de dispositif optique qui permet d'observer ce type de franges, les conditions d'éclairage nécessaires, et préciser à quel endroit les franges sont localisées.
Voir la solution


![\includegraphics[width=7cm]{biprism1.eps}](img48.png)
![\includegraphics[width=19cm]{frprism.eps}](img49.png)
![]() et d'amplitude
et d'amplitude ![]() Ce biprisme est placé dans le plan
Ce biprisme est placé dans le plan ![]() , on observe dans le plan
, on observe dans le plan ![]() . Là encore, on négligera la diffraction par les bords des prismes.
. Là encore, on négligera la diffraction par les bords des prismes.
![\includegraphics[width=7cm]{biprism2.eps}](img62.png) 6
6
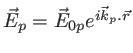 à la sortie du biprisme. Préciser leur amplitude
à la sortie du biprisme. Préciser leur amplitude