Licence de Physique -- Second partiel d'optique II
Documents: feuille A4 RV manuscrite + formulaire de TF - durée 2h
Date: 17 Décembre 2008
L'interféromètre de Mach-Zehnder est représenté ci-dessous. Comme dans le Michelson, l'onde incidente est séparée en deux ondes par une lame séparatrice 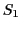 de de coefficient de réflexion
de de coefficient de réflexion 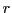 et de transmission
et de transmission 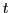 égaux. L'onde 1 se réfléchit sur le miroir
égaux. L'onde 1 se réfléchit sur le miroir 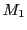 faisant un angle de 45
faisant un angle de 45 par rapport à la direction de propagation, puis éclaire une seconde lame séparatrice
par rapport à la direction de propagation, puis éclaire une seconde lame séparatrice 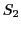 identique à
identique à 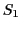 , qui transmet une partie de l'onde vers l'écran d'observation
, qui transmet une partie de l'onde vers l'écran d'observation 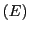 . On nomme ``bras 1'' de l'interféromètre le trajet
. On nomme ``bras 1'' de l'interféromètre le trajet
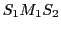 . L'onde 2 se réfléchit sur un miroir
. L'onde 2 se réfléchit sur un miroir 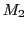 incliné de
incliné de
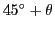 . Une partie de l'onde est ensuite réfléchie vers l'écran d'observation
. Une partie de l'onde est ensuite réfléchie vers l'écran d'observation 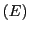 , elle arrive sur cet écran avec un angle incidence
, elle arrive sur cet écran avec un angle incidence 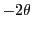 (voir schéma). On nomme ``bras 2'' le trajet
(voir schéma). On nomme ``bras 2'' le trajet
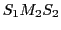 . On observe l'interférence des deux ondes 1 et 2 en un point
. On observe l'interférence des deux ondes 1 et 2 en un point 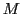 de coordonnées x,y sur l'écran
de coordonnées x,y sur l'écran 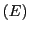 . On pose
. On pose 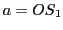 ,
,
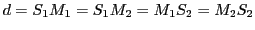 et
et 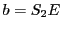 . On suppose
. On suppose
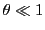 (approximation paraxiale).
(approximation paraxiale).
Cet interféromètre est éclairé par une onde plane arrivant sous incidence normale (direction de propagation 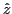 ).
).
- La lumière est monochromatique de longueur d'onde
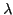 et d'amplitude
et d'amplitude 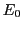 dans le plan
dans le plan 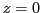 . on se place dans l'hypothèse du champ scalaire (on ne s'occupe pas des directions des champs électriques, comme dans le premier chapitre du cours).
. on se place dans l'hypothèse du champ scalaire (on ne s'occupe pas des directions des champs électriques, comme dans le premier chapitre du cours).
- Ecrire l'amplitude complexe des ondes 1 et 2 au point
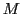
- En déduire l'intensité, donner l'interfrange et le contraste des franges.
- La lumière est toujours monochromatique mais non polarisée (lumière naturelle). A l'entrée de l'interféromètre, dans le plan
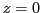 , on place un polariseur
, on place un polariseur 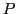 dont la direction
dont la direction 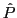 fait un angle de 45
fait un angle de 45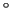 avec
avec 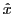 , soit
, soit
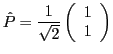 . On place dans le bras 1 une lame anisotrope
. On place dans le bras 1 une lame anisotrope 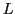 à faces parallèles, d'épaisseur
à faces parallèles, d'épaisseur 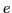 , dont l'axe optique est parallèle à
, dont l'axe optique est parallèle à 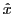 . La lame est éclairée sous incidence normale, les indices ordinaire et extraordinaire sont nommés respectivement no et ne
. La lame est éclairée sous incidence normale, les indices ordinaire et extraordinaire sont nommés respectivement no et ne
- Ecrire le champ électrique
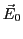 de l'onde incidente en z=0+
après traversée du polariseur
de l'onde incidente en z=0+
après traversée du polariseur 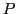 (on pourra omettre la dépendance temporelle
(on pourra omettre la dépendance temporelle
 et on appellera
et on appellera 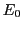 l'amplitude du champ en z=0+).
l'amplitude du champ en z=0+).
- Ecrire le champ électrique
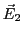 de l'onde 2 en
de l'onde 2 en 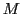 .
.
- Ecrire les déphasages induits par la lame
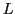 sur les deux composantes
sur les deux composantes 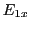 et
et 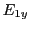 du champ électrique
du champ électrique 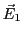 de l'onde 1. En déduire l'expression de
de l'onde 1. En déduire l'expression de 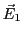 en
en 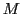 .
.
- Que doit valoir
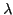 pour que l'onde 1 soit circulaire gauche (on appellera
pour que l'onde 1 soit circulaire gauche (on appellera 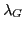 cette valeur) ?
cette valeur) ?
- Si on tourne la lame
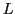 de 90
de 90 de sorte que l'axe optique soit parallèle à
de sorte que l'axe optique soit parallèle à 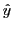 , l'onde 1 sera-t-elle toujours circulaire gauche pour la longueur d'onde
, l'onde 1 sera-t-elle toujours circulaire gauche pour la longueur d'onde 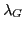 de la question précédente ? Sinon, préciser son état de polarisation.
de la question précédente ? Sinon, préciser son état de polarisation.
- On se place dans le cas où no=ne
(
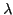 est ici quelconque). Comment s'écrit l'intensité en
est ici quelconque). Comment s'écrit l'intensité en 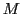 dans ce cas ? Qu'est-ce qui a changé par rapport à la question 1 ? Que se passe-t-il si on tourne le polariseur
dans ce cas ? Qu'est-ce qui a changé par rapport à la question 1 ? Que se passe-t-il si on tourne le polariseur 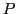 dans le plan
dans le plan 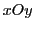 ?
?
- On se place à la longueur d'onde
 . Calculer le champ
. Calculer le champ 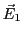 en
en 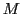 , faire un schéma montrant l'orientation des vecteurs
, faire un schéma montrant l'orientation des vecteurs
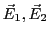 et
et 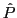 dans le plan
dans le plan 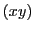 . Calculer l'intensité en
. Calculer l'intensité en 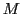 , décrire l'image dans le plan
, décrire l'image dans le plan 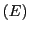 , préciser son contraste.
, préciser son contraste.
- Même question si
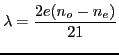
Voir la solution
Un objet périodique spatialement incohérent émet par unité de surface une intensité
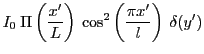 (distribution spatiale d'intensité ou de brillance) où
(distribution spatiale d'intensité ou de brillance) où 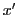 et
et 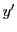 représentent les coordonnées dans le plan de l'objet. On suppose
représentent les coordonnées dans le plan de l'objet. On suppose 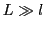 . Cet objet est placé à très grande distance (considéré comme à l'infini)
. Cet objet est placé à très grande distance (considéré comme à l'infini) 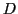 d'une paire de trous d'Young ponctuels alignés dans la direction
d'une paire de trous d'Young ponctuels alignés dans la direction  et séparés de
et séparés de 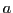 (les directions
(les directions  et
et 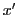 sont parallèles). On observe les franges sur un écran
sont parallèles). On observe les franges sur un écran 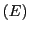 placé à grande distance
placé à grande distance 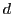 du plan des trous. On se place dans l'approximation paraxiale.
du plan des trous. On se place dans l'approximation paraxiale.
![\includegraphics[width=12cm]{cspat.eps}](img68.png)
- Ecrire la distribution angulaire de brillance
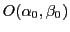 de cet objet (
de cet objet (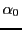 et
et 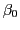 sont les angles associés aux directions
sont les angles associés aux directions 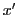 et
et 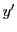 ).
).
- Calculer la transformée de Fourier
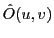 de
de
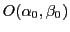 Tracer le graphe de la fonction
Tracer le graphe de la fonction
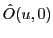 (on suppose
(on suppose 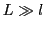 ).
).
- Relier le contraste
 des franges d'Young dans le plan
des franges d'Young dans le plan 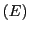 à la la transformée de Fourier de
à la la transformée de Fourier de
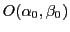 (on rappelle que
(on rappelle que 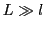 )
)
- Montrer qu'on n'observe des franges d'interférences qu'au voisinage de 2 valeurs
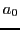 et
et 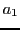 de la séparation
de la séparation 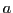 des trous (
des trous (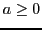 ).
).
- On réalise a=a1. Ecrire l'intensité
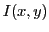 des franges d'Young en un point de coordonnées
des franges d'Young en un point de coordonnées  dans le plan
dans le plan 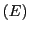 . Tracer le graphe de
. Tracer le graphe de 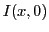 et préciser le contraste des franges.
et préciser le contraste des franges.
Voir la solution
![\includegraphics[width=14cm]{mczender.eps}](img19.png)
![\includegraphics[width=14cm]{mczender.eps}](img19.png)
![]() ).
).
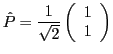 . On place dans le bras 1 une lame anisotrope
. On place dans le bras 1 une lame anisotrope  . Calculer le champ
. Calculer le champ 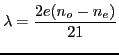
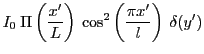 (distribution spatiale d'intensité ou de brillance) où
(distribution spatiale d'intensité ou de brillance) où ![\includegraphics[width=12cm]{cspat.eps}](img68.png)