Licence de Physique -- Second partiel d'optique
Durée 2 h
Date: Documents autorisés : formulaire de TF +
1 feuille A4 manuscrite recto-verso
Le dispositif ci-dessous est constitué de deux prismes accolés (angle
de 45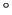 ),
taillés dans le même matériau uniaxe parfaitement diélectrique. Les
axes optiques sont orthogonaux entre eux. L'axe du premier prisme est
parallèle à la direction
),
taillés dans le même matériau uniaxe parfaitement diélectrique. Les
axes optiques sont orthogonaux entre eux. L'axe du premier prisme est
parallèle à la direction 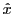 , l'axe du second à la direction
, l'axe du second à la direction 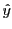 . Les indices ordinaire et extraordinaire sont notés
. Les indices ordinaire et extraordinaire sont notés 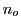 et
et 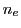 , on suppose
, on suppose 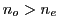 . Ce prisme est plongé dans le vide (indice
. Ce prisme est plongé dans le vide (indice 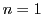 ). Il est éclairé sous incidence normale par une onde monochromatique
non polarisée, de longueur d'onde
). Il est éclairé sous incidence normale par une onde monochromatique
non polarisée, de longueur d'onde 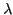 dans le vide, se
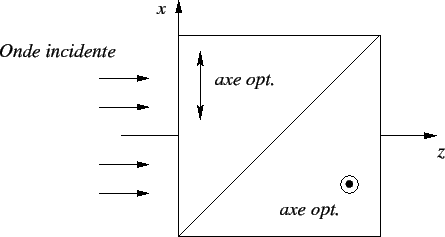
propageant dans la direction
dans le vide, se
propageant dans la direction 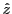 .
.
- Qu'appelle-t-on une onde non polarisée ?
- Qu'est-ce qu'un matériau uniaxe ?
- Pour quelle raison le vecteur déplacement électrique
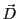 est-il contenu dans un plan (que l'on précisera) ?
est-il contenu dans un plan (que l'on précisera) ?
- Décomposer le vecteur
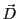 en deux
polarisations orthogonales
en deux
polarisations orthogonales 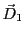 et
et 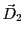 . Préciser les directions de
. Préciser les directions de 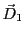 et
et 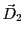 .
.
- Pour l'onde correspondant à la polarisation
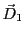 , faire le tracé des rayons réfractés sur chaque face (construction de
Descartes) et calculer l'angle d'émergence (angle entre l'axe
, faire le tracé des rayons réfractés sur chaque face (construction de
Descartes) et calculer l'angle d'émergence (angle entre l'axe 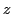 et la direction du rayon en sortie de la dernière face).
Donner l'expression du vecteur d'onde associé à
et la direction du rayon en sortie de la dernière face).
Donner l'expression du vecteur d'onde associé à 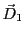 dans chaque milieu.
dans chaque milieu.
- Même question pour l'onde correspondant à la polarisation
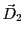 .
.
- Calculer ces angles dans le cas de la calcite :
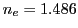 ,
, 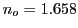 .
.
- A quelle condition sur
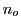 et
et 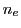 n'a-t-on qu'un seul rayon en sortie (indication : considérer la
réfraction sur la face inclinée à 45 degrés qui sépare les prismes) ?
Pourquoi dit-on dans ce cas que le Wollaston se comporte comme un
polariseur ?
n'a-t-on qu'un seul rayon en sortie (indication : considérer la
réfraction sur la face inclinée à 45 degrés qui sépare les prismes) ?
Pourquoi dit-on dans ce cas que le Wollaston se comporte comme un
polariseur ?
Un interféromètre de Michelson est éclairé par une onde plane arrivant
parallèlement à la direction 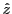 . Les interférences sont observées en un point
. Les interférences sont observées en un point 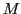 de
coordonnées
de
coordonnées  dans le plan
dans le plan 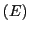 de la
figure ci-après. On pose
de la
figure ci-après. On pose 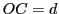 ,
, 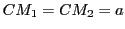 et
et 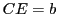 et
et 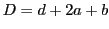 . Le miroir
. Le miroir  est éclairé sour incidence normale. Le miroir
est éclairé sour incidence normale. Le miroir 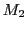 est incliné d'un angle
est incliné d'un angle 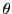 (michelson réglé en coin d'air). La lame séparatrice est supposée
d'épaisseur nulle et de coefficient de réflexion en amplitude
(michelson réglé en coin d'air). La lame séparatrice est supposée
d'épaisseur nulle et de coefficient de réflexion en amplitude 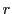 et de transmission
et de transmission 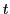 .
.
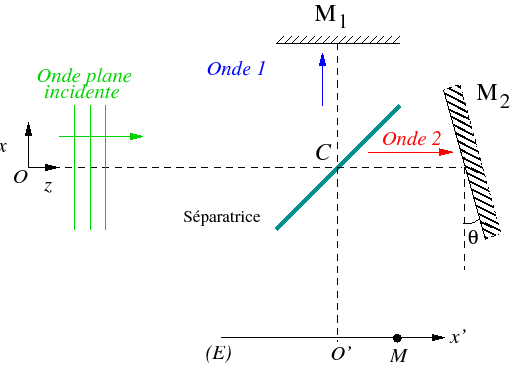
- Remplacez le Michelson par un schéma équivalent plus simple.
- L'onde incidente est monochromatique de longueur d'onde
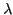 et d'amplitude
et d'amplitude 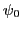 dans le plan
dans le plan 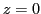 .
.
- Quelle est la signification physique de la longueur de
cohérence
d'une onde ? Que vaut-elle dans le cas parfaitement
monochromatique ?
- Ecrire l'amplitude complexe
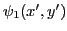 et
et 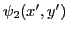 des ondes qui interfèrent au point
des ondes qui interfèrent au point 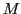
- En déduire l'intensité lumineuse
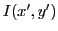 . Décrire la figure observée
. Décrire la figure observée
- Calculer l'interfrange et le contraste des franges
- Ecrire la différence de marche entre les deux ondes
 et
et 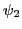
- En déduire le retard
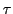 entre ces ondes et
réécrire l'expression de l'intensité en fonction de
entre ces ondes et
réécrire l'expression de l'intensité en fonction de 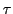 .
.
- (Les questions (a) à (d) sont indépendantes de la question 2).
L'onde incidente est quasi-monochromatique, de fréquence moyenne
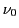 , de profil
, de profil 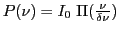 avec
avec
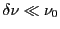 la largeur de
la largeur de  (largeur de bande). On pose
(largeur de bande). On pose 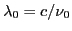 et
et 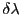 la largeur de bande exprimée en longueur
d'onde.
la largeur de bande exprimée en longueur
d'onde.
- Rappeler ce que représente le spectre
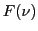 d'une onde.
d'une onde.
- Que vaut
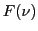 dans notre cas ? Tracez l'allure de
son graphe.
dans notre cas ? Tracez l'allure de
son graphe.
- Quelle est la longueur de cohérence
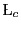 de
l'onde ? A.N. :
de
l'onde ? A.N. : 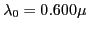 m,
m, 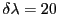 nm.
nm.
- Calculer le degré complexe de cohérence de l'onde.
- En déduire l'intensité au point
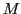 en
fonction de la variable
en
fonction de la variable 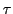 (retard
(retard 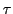 entre les 2 ondes).
entre les 2 ondes).
- Donner l'expression de la fonction contraste
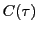 et tracer son graphe
et tracer son graphe
- Tracez l'intensité en fonction de
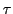 .
.
- Partant de
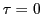 , pour quelle valeur
, pour quelle valeur 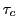 de
de 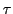 observe-t-on une première fois la disparition des
franges ? On appelle ``paquet central de franges'' l'intervalle
observe-t-on une première fois la disparition des
franges ? On appelle ``paquet central de franges'' l'intervalle
![$ [-\tau_c,\tau_c]$](img51.png) .
.
- Quelle est la signification physique de
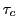 ?
?
- Combien de franges seront visibles dans le paquet central ?
A.N.
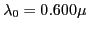 m,
m, 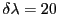 nm ?
nm ?
- Que vaut l'interfrange
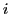 (en mètres dans le
plan
(en mètres dans le
plan 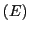 ) ? A.N.
) ? A.N. 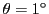
- Quelle est la taille, en mètres dans le plan
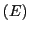 , du paquet central de franges ? A.N. (mêmes valeurs)
, du paquet central de franges ? A.N. (mêmes valeurs)
Voir la solution


