L3 Physique -- Examen partiel d'optique
24 Février 2016
Durée 1h30. Document autorisé : formulaire de TF, autres documents interdits. Calculette autorisée, téléphone interdit
- Un laser éclaire uniformément un trou carré de côté
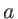 =0.1 mm. La puissance lumineuse totale qui traverse le trou est de 0.1 mW. Quelle est l'intensité lumineuse de l'onde en sortie du trou ?
=0.1 mm. La puissance lumineuse totale qui traverse le trou est de 0.1 mW. Quelle est l'intensité lumineuse de l'onde en sortie du trou ?
- Rappeler la relation qui lie la focale d'une lentille plan-convexe à son indice de réfraction et son rayon de courbure. Une lentille plan-convexe est taillée dans un matériau d'indice
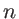 qui dépend de la longueur d'onde :
qui dépend de la longueur d'onde :
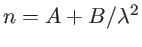 avec
avec 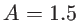 ,
,
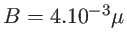 m
m . La focale est
. La focale est 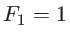 m pour la longueur d'onde
m pour la longueur d'onde
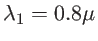 m. Quelle est la focale
m. Quelle est la focale 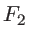 pour la longueur d'onde
pour la longueur d'onde
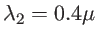 m ?
m ?
- L'image ci-dessous montre l'intensité diffractée par une fente, dans l'approximation de Fraunhofer (champ lointain). La longueur d'onde est
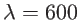 nm, la distance entre la fente et le plan d'observation est
nm, la distance entre la fente et le plan d'observation est 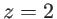 m. Le lobe central de la figure de diffraction a une taille de 24 mm. Quelle est la largeur de la fente ?
m. Le lobe central de la figure de diffraction a une taille de 24 mm. Quelle est la largeur de la fente ?
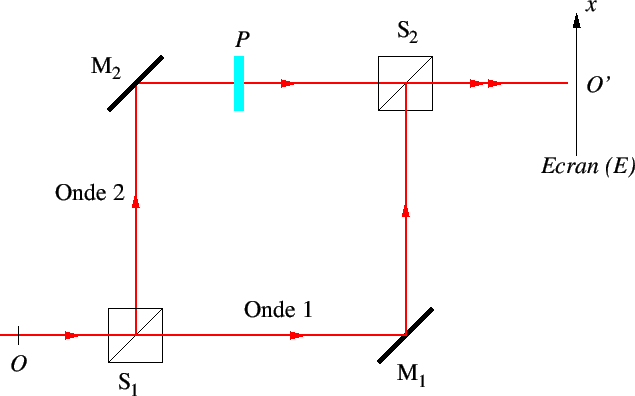
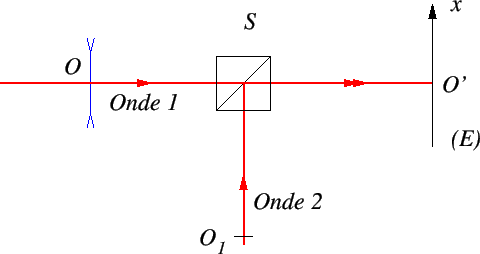
Le schéma-ci-dessus est un interféromètre de Mach-Zehnder. L'onde incidente (au point 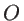 ) est plane et se propage parallèllement à la direction
) est plane et se propage parallèllement à la direction 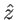 . Elle a une amplitude
. Elle a une amplitude  et une longueur d'onde
et une longueur d'onde  . Une lame semi-réfléchissante
. Une lame semi-réfléchissante 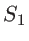 la sépare en deux ondes (1 et 2). L'onde 1 éclaire un miroir
la sépare en deux ondes (1 et 2). L'onde 1 éclaire un miroir 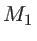 totalement réfléchissant puis se réfléchit sur une seconde lame semi-réfléchissante
totalement réfléchissant puis se réfléchit sur une seconde lame semi-réfléchissante 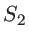 identique à
identique à 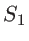 . L'onde 2 éclaire un miroir
. L'onde 2 éclaire un miroir 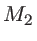 totalement réfléchissant puis traverse la lame
totalement réfléchissant puis traverse la lame 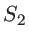 . Entre
. Entre 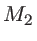 et
et 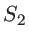 on intercale une lame à faces parallèles
on intercale une lame à faces parallèles 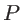 d'indice de réfraction
d'indice de réfraction 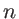 , et d'épaisseur constante
, et d'épaisseur constante
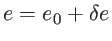 , avec
, avec 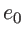 parfaitement connu, et
parfaitement connu, et 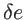 une quantité faible (inférieure à
une quantité faible (inférieure à  ) inconnue. On observe l'interférence des deux ondes sur l'écran
) inconnue. On observe l'interférence des deux ondes sur l'écran 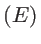 . On note
. On note 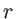 et
et 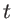 les coefficients de transmission (en amplitude) des lames
les coefficients de transmission (en amplitude) des lames 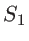 et
et 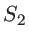 . On appelle
. On appelle 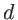 la distance
la distance
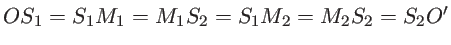 .
.
- Remplacer ce problème par un schéma équivalent plus simple, pour l'onde 1 et pour l'onde 2.
- On enlève la lame
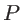 :
:
- Ecrire l'amplitude complexe de l'onde 1 sur l'écran
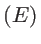 . Faites de même pour l'onde 2
. Faites de même pour l'onde 2
- Calculer l'intensité
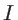 sur l'écran, et décrire l'image observée.
sur l'écran, et décrire l'image observée.
- On replace maintenant la lame. Ecrire l'amplitude complexe de l'onde 2 sur l'écran
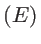 .
.
- Calculer la nouvelle intensité
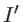 sur l'écran
sur l'écran 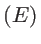 .
.
- A partir des intensités en présence et en l'absence de la lame, proposer une méthode pour mesurer
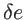 (on fera l'hypothèse que la quantité
(on fera l'hypothèse que la quantité 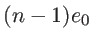 est un multiple de
est un multiple de  ).
).
Pour tout l'exercice on se place dans l'approximation paraxiale.
Questions préliminaires :
- Une lentille divergente de focale
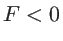 , placée dans le plan
, placée dans le plan 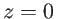 , est éclairée sous incidence normale par une onde plane d'amplitude
, est éclairée sous incidence normale par une onde plane d'amplitude  et de longueur d'onde
et de longueur d'onde  , se propageant vers les
, se propageant vers les 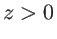 . Ecrire l'amplitude complexe
. Ecrire l'amplitude complexe 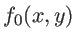 de l'onde dans le plan
de l'onde dans le plan 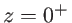 en sortie de la lentille
en sortie de la lentille
- De quel type d'onde s'agit-il, et pourquoi ?
- Donner la position de la source de cette onde.
- En déduire l'amplitude complexe
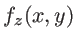 de l'onde dans un plan
de l'onde dans un plan 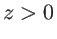 quelconque. Faire apparaitre la constante
quelconque. Faire apparaitre la constante  dans l'expression de
dans l'expression de 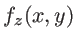 .
.
On fait interférer l'onde en sortie de la lentille avec une onde plane. Pour celà, on réalise le montage ci-dessus. l'onde 1 provenant de la lentille traverse une lame séparatrice 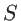 . Une seconde onde (onde 2 sur le schéma), plane, a une amplitude
. Une seconde onde (onde 2 sur le schéma), plane, a une amplitude  au point
au point 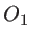 . Elle se réfléchit sur la séparatrice
. Elle se réfléchit sur la séparatrice 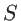 , puis se propage parallèllement à l'axe
, puis se propage parallèllement à l'axe 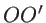 jusqu'à l'écran
jusqu'à l'écran 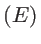 . On appelle
. On appelle 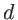 la distance
la distance 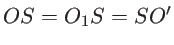 . Les coefficients de transmission (en amplitude)
. Les coefficients de transmission (en amplitude) 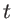 et de réflexion
et de réflexion 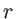 de la séparatrice
de la séparatrice 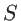 sont supposés réels, avec
sont supposés réels, avec 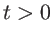 et
et 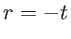 .
.
- Ecrire l'amplitude complexe de l'onde 1 sur l'écran
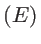 (utiliser le résultat de la question 4)
(utiliser le résultat de la question 4)
- Même question pour l'onde 2
Questions bonus hors-barème :
- Calculer l'intensité sur l'écran
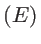
- Tracer le graphe de l'intensité et décrire l'image observée : voit-on une teinte plate, des franges, des anneaux, des pics, ou autre chose ?
- Calculer le contraste de l'intensité.
Voir la solution



![]() ) est plane et se propage parallèllement à la direction
) est plane et se propage parallèllement à la direction ![]() . Elle a une amplitude
. Elle a une amplitude ![]() et une longueur d'onde
et une longueur d'onde ![]() . Une lame semi-réfléchissante
. Une lame semi-réfléchissante ![]() la sépare en deux ondes (1 et 2). L'onde 1 éclaire un miroir
la sépare en deux ondes (1 et 2). L'onde 1 éclaire un miroir ![]() totalement réfléchissant puis se réfléchit sur une seconde lame semi-réfléchissante
totalement réfléchissant puis se réfléchit sur une seconde lame semi-réfléchissante ![]() identique à
identique à ![]() . L'onde 2 éclaire un miroir
. L'onde 2 éclaire un miroir ![]() totalement réfléchissant puis traverse la lame
totalement réfléchissant puis traverse la lame ![]() . Entre
. Entre ![]() et
et ![]() on intercale une lame à faces parallèles
on intercale une lame à faces parallèles ![]() d'indice de réfraction
d'indice de réfraction ![]() , et d'épaisseur constante
, et d'épaisseur constante
![]() , avec
, avec ![]() parfaitement connu, et
parfaitement connu, et ![]() une quantité faible (inférieure à
une quantité faible (inférieure à ![]() ) inconnue. On observe l'interférence des deux ondes sur l'écran
) inconnue. On observe l'interférence des deux ondes sur l'écran ![]() . On note
. On note ![]() et
et ![]() les coefficients de transmission (en amplitude) des lames
les coefficients de transmission (en amplitude) des lames ![]() et
et ![]() . On appelle
. On appelle ![]() la distance
la distance
![]() .
.