Licence de Physique -- Examen d'optique II
Session de Janvier 2009
Date: Documents: feuille A4 RV manuscrite + formulaire de TF - durée 3h
On condidère une source ponctuelle 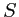 placée au dessus d'un miroir parfaitement réfléchissant (coefficient de réflexion
placée au dessus d'un miroir parfaitement réfléchissant (coefficient de réflexion 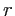 tel que
tel que 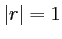 ). C'est l'interféromètre à miroir de Lloyd. Le miroir est confondu avec le plan
). C'est l'interféromètre à miroir de Lloyd. Le miroir est confondu avec le plan 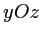 , on appelle (
, on appelle (
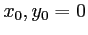 ) les coordonnées de la source
) les coordonnées de la source 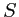 dans le plan de la source (
dans le plan de la source (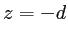 ). Un écran
). Un écran 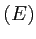 est placé à une distance
est placé à une distance 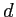 de la source (plan
de la source (plan 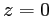 ). Sur cet écran on observe les interférences lumineuses produites en un point de coordonnées
). Sur cet écran on observe les interférences lumineuses produites en un point de coordonnées 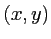 par la source
par la source 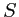 et par son image dans le miroir (les ondes correspondantes sont appellées ``onde 1'' et ``onde 2'' sur le schéma ci-dessous). On note
et par son image dans le miroir (les ondes correspondantes sont appellées ``onde 1'' et ``onde 2'' sur le schéma ci-dessous). On note 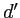 la distance entre le point du miroir où se réfléchit le rayon provenant de
la distance entre le point du miroir où se réfléchit le rayon provenant de 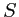 et l'écran
et l'écran 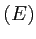 . Dans tout le problème on se place dans l'approximation paraxiale :
. Dans tout le problème on se place dans l'approximation paraxiale : 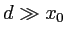 ,
, 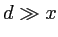 .
.
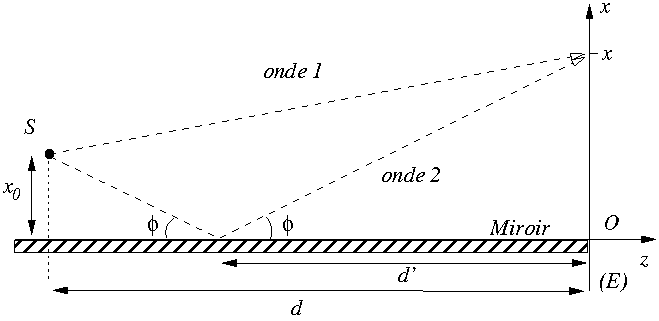
- (Question indépendante des suivantes) Sachant que les angles que font un rayon incident et réfléchi avec le miroir sont les mêmes, calculer
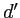 en fonction de
en fonction de 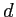 ,
, 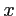 et
et 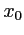 .
.
- Ce problème a un schéma équivalent plus simple, faisant intervenir deux sources ponctuelles
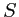 et
et 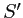 . Calculer la position
. Calculer la position
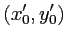 de la source
de la source 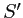 et faire le schéma équivalent. A quel type de système interférentiel ce schéma vous fait-il penser ?
et faire le schéma équivalent. A quel type de système interférentiel ce schéma vous fait-il penser ?
- Sachant que la réflexion sur le miroir provoque une déphasage de
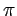 , prédire sans calcul (mais en justifiant votre réponse par des arguments physiques) si le point
, prédire sans calcul (mais en justifiant votre réponse par des arguments physiques) si le point 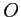 est sur une frange brillante ou sur une frange sombre.
est sur une frange brillante ou sur une frange sombre.
- La source est monochromatique, de fréquence
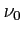 , de longueur d'onde
, de longueur d'onde 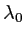 et d'amplitude
et d'amplitude 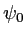 . Calculer l'intensité des franges sur l'écran
. Calculer l'intensité des franges sur l'écran 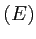 en fonction de
en fonction de 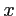 . Donner l'interfrange et le contraste de la figure.
. Donner l'interfrange et le contraste de la figure.
- La source est quasi-monochromatique. Son spectre
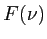 en fonction de la fréquence
en fonction de la fréquence 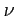 est donné par une fonction Lorentzienne
est donné par une fonction Lorentzienne
avec 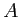 ,
, 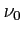 et
et 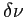 des constantes positives et
des constantes positives et
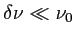 .
.
- Calculer le degré complexe de cohérence de l'onde
- En déduire l'intensité des franges sur l'écran
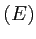 en fonction de
en fonction de 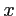
- Quelles sont les régions de l'écran
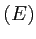 pour lesquelles le contraste de l'intensité est supérieur à
pour lesquelles le contraste de l'intensité est supérieur à 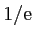 en valeur absolue ? Combien y-a-t-il de franges visibles dans cette région ?
en valeur absolue ? Combien y-a-t-il de franges visibles dans cette région ?
- La source
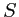 est à nouveau monochromatique. On place une seconde source
est à nouveau monochromatique. On place une seconde source 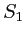 , identique à la première, décalée dans la direction
, identique à la première, décalée dans la direction 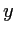 . La position de
. La position de 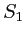 dans le plan
dans le plan 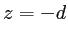 est repérée par les coordonnées
est repérée par les coordonnées
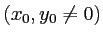 . Les deux sources
. Les deux sources 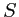 et
et 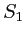 sont incohérentes entre elles.
sont incohérentes entre elles.
- On enlève la première source
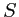 . Calculer l'intensité sur l'écran
. Calculer l'intensité sur l'écran 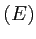 en fonction de
en fonction de 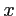 . Comparer au résultat de la question 4.
. Comparer au résultat de la question 4.
- On remet la source
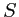 : Calculer l'intensité sur l'écran
: Calculer l'intensité sur l'écran 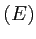 . Commentaires ?
. Commentaires ?
Un télescope est un dispositif à miroir concave de section circulaire qui forme en son plan focal l'image d'un objet à l'infini, comme le ferait une lentille convergente.
- Rappeler l'allure de la figure de diffraction à l'infini (intensité
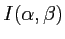 en fonction des directions
en fonction des directions 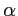 et
et 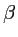 ) produite par un diaphragme circulaire de diamètre
) produite par un diaphragme circulaire de diamètre 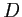 éclairé sous incidence normale par une onde plane de longueur
éclairé sous incidence normale par une onde plane de longueur 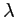 . On se place dans l'approximation paraxiale. Faire un dessin portant les mentions jugées nécessaires. Que vaut l'intensité
. On se place dans l'approximation paraxiale. Faire un dessin portant les mentions jugées nécessaires. Que vaut l'intensité 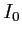 au centre (on rappelle que
au centre (on rappelle que
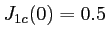 ) ?
) ?
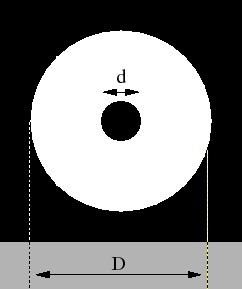
- En réalité, le télescope est équipé d'un petit miroir secondaire qui sert à dévier la lumière sur le côté de l'appareil. Ce miroir secondaire occulte la partie centrale du miroir principal ; ce dispositif peut ètre modélisé par un écran constitué d'une ouverture circulaire occultée en son centre par un disque opaque de diamètre
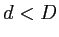 (voir figure ci-dessous). Ecrire le coefficient de transmission de cet écran.
(voir figure ci-dessous). Ecrire le coefficient de transmission de cet écran.
- Ecrire l'amplitude diffractée à l'infini si cet écran est éclairé normalement par une onde plane
(incidence normale) de longueur d'onde
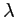 .
.
- Faire un graphe de l'amplitude dans le cas où
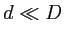 . Comment est modifié ce graphe par rapport à la situation sans obstruction centrale de la question 1 ?
. Comment est modifié ce graphe par rapport à la situation sans obstruction centrale de la question 1 ?
- Comment faut-il choisir
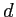 pour que l'intensité au centre subisse une baisse inférieure à 10% par rapport à la question 1 ?
pour que l'intensité au centre subisse une baisse inférieure à 10% par rapport à la question 1 ?
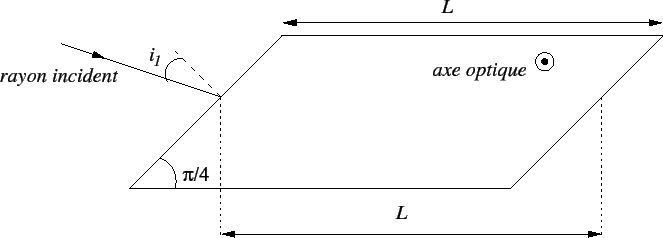
Soit un prisme de calcite possédant la géométrie de la figure ci-dessous : les faces inférieure et supérieure sont horizontales, les faces latérales (droite et gauche) sont parallèles entre elles et font un angle de 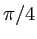 avec l'horizontale. Le prisme est de longueur
avec l'horizontale. Le prisme est de longueur 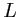 , il est plongé dans l'air (indice
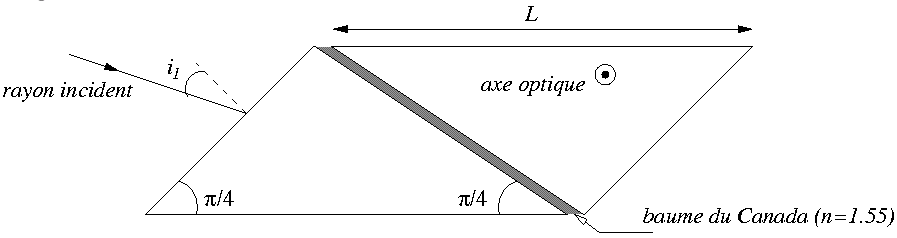
, il est plongé dans l'air (indice 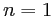 ). Une onde plane non polarisée éclaire le prisme en faisant un angle d'incidence
). Une onde plane non polarisée éclaire le prisme en faisant un angle d'incidence 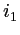 avec la normale L'axe optique du prisme est perpendiculaire au plan d'incidence, les indices ordinaire et extraordinaire sont notés
avec la normale L'axe optique du prisme est perpendiculaire au plan d'incidence, les indices ordinaire et extraordinaire sont notés 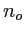 et
et 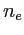 respectivement. Les valeurs pour la calcite sont
respectivement. Les valeurs pour la calcite sont 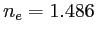 ,
, 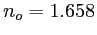 .
.
- Faire un schéma montrant la trajectoire des rayons ordinaire et extraordinaire à l'intérieur du prisme (on suppose que les 2 rayons touchent la seconde face). Préciser les polarisations (directions de
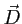 ) pour les deux rayons.
) pour les deux rayons.
- Calculer les angles que font les rayons réfractés par la première face avec sa normale. A.N.:
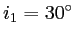
- Montrer qu'à la sortie du prisme (après la 2e face), les rayons ordinaire et extraordinaire sont parallèles entre eux mais décalés d'une quantité
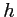 que l'on calculera (
que l'on calculera (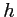 est mesuré dans la direction verticale). Quel est l'angle que font ces rayons avec la normale à la 2e face ? A.N.:
est mesuré dans la direction verticale). Quel est l'angle que font ces rayons avec la normale à la 2e face ? A.N.:
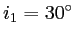 ,
, 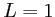 cm.
cm.
- On découpe maintenant ce prisme selon la diagonale et on écarte les deux moitiés pour laisser une mince lame dans laquelle on injecte du baume du Canada d'indice
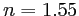 , comme dans la figure ci-dessous.
, comme dans la figure ci-dessous.
Faire le tracé des rayons ordinaire et extraordinaire jusqu'à la lame de baume du Canada et préciser les angles 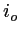 et
et 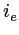 que font les rayons ordinaire et extraordinaire avec la normale à la lame (comme dans le cas précédent, on suppose que les 2 rayons touchent la lame de baume du Canada). A.N.:
que font les rayons ordinaire et extraordinaire avec la normale à la lame (comme dans le cas précédent, on suppose que les 2 rayons touchent la lame de baume du Canada). A.N.:
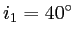 et
et
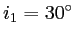 .
.
- Quelle est la condition sur
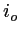 pour que le rayon ordinaire soit réfléchi totalement par la lame de baume du Canada ? Même question pour le rayon extraordinaire.
pour que le rayon ordinaire soit réfléchi totalement par la lame de baume du Canada ? Même question pour le rayon extraordinaire.
- En déduire la valeur maximale
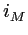 que doit prendre
que doit prendre 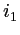 pour que seul l'un des deux rayons soit transmis par la lame de Baume du Canada. Faire l'application numérique avec les valeurs des indices de la calcite. Préciser la polarisation transmise.
pour que seul l'un des deux rayons soit transmis par la lame de Baume du Canada. Faire l'application numérique avec les valeurs des indices de la calcite. Préciser la polarisation transmise.
- Question bonus hors barème : A votre avis, a quoi sert le second prisme (indication : on pourra s'intéresser à l'angle d'incidence du rayon réfracté à la sortie du 2e prisme).
Le baume du Canada, appelé aussi térébenthine du Canada ou gomme de sapin, est une térébenthine issue de la résine du sapin baumier. La résine, dissoute dans des huiles essentielles, est visqueuse, collante et incolore (parfois jaunâtre) après évaporation des huiles essentielles.
Grâce à sa grande qualité de transparence et à son indice de réfraction (1,55) proche de celui du verre, ce baume est surtout utilisé en optique pour accoler des objets de verre dans certains prismes ou polariseurs. Il est soluble dans le xylène, amorphe lorsqu'il est séché, et il ne cristallise pas avec l'âge. Il est aussi utilisé en biologie pour conserver des échantillons de microscopie, pour réparer des fissures sur le verre (comme des pare-brise) ou en peinture à l'huile. (Extrait de Wikipedia).
Voir la solution