L3 Physique -- Examen d'optique 2e session
Durée 3 h
Date: Documents autorisés : formulaire de TF +
1 feuille A4 manuscrite recto-verso
Une source ponctuelle monochromatique (amplitude 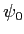 , longueur d'onde
, longueur d'onde 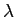 ) se trouve au point de coordonnées
) se trouve au point de coordonnées  . Dans le plan
. Dans le plan 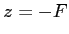 se trouve une lentille convergente
de focale
se trouve une lentille convergente
de focale 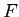 et de dimensions transversales supposées
infinies. Dans le plan
et de dimensions transversales supposées
infinies. Dans le plan 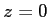 on place un réseau de fentes très
fines (leur largeur est assimilée à 0), de période
on place un réseau de fentes très
fines (leur largeur est assimilée à 0), de période 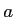 dans la
direction
dans la
direction 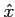 et invariant par translation dans la direction
et invariant par translation dans la direction
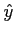 . Le réseau est lui aussi de dimensions infinies. L'ensemble est
schématisé ci-dessous.
. Le réseau est lui aussi de dimensions infinies. L'ensemble est
schématisé ci-dessous.
- Quelle est la nature de l'onde dans la région
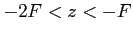 ?
?
- Ecrire, sans faire l'approximation paraxiale, l'amplitude
complexe de l'onde dans cette région.
- Réécrire cette amplitude complexe dans l'approximation paraxiale.
Dans toute la suite du problème on se place dans les conditions
paraxiales.
- (Question indépendante) Rappeler en quoi consiste cette
approximation
- Ecrire l'amplitude complexe de l'onde en
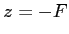 juste
avant la traversée de la lentille
juste
avant la traversée de la lentille
- Ecrire le coefficient de transmission de la lentille
- Ecrire l'amplitude complexe de l'onde en
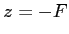 juste
après la lentille
juste
après la lentille
- Quelle est la nature de cette onde ?
- Ecrire l'amplitude complexe en
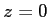 juste avant la
traversée du réseau
juste avant la
traversée du réseau
- Ecrire l'intensité
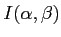 diffractée à l'infini par le réseau dans une
direction
diffractée à l'infini par le réseau dans une
direction 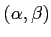 .
.
- (Question indépendante) Rappeler ce qu'on appelle ordre de
diffraction d'un réseau.
- Dans quelle direction
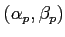 se trouve l'ordre
se trouve l'ordre 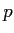 ?
?
- Reprendre les questions 2,3,5,7,9,10,12 dans le cas où la source
est déplacée au point
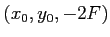 .
.
On complète le montage précédent par une lentille convergente de focale
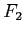 située dans le plan
située dans le plan 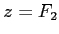 . La source est à nouveau en
. La source est à nouveau en  . On place un écran d'observation dans le plan
. On place un écran d'observation dans le plan 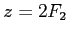 (plan focal image de la deuxième lentille). On est toujours dans
l'approximation paraxiale. Le nouveau montage est celui de la figure
ci-dessous.
(plan focal image de la deuxième lentille). On est toujours dans
l'approximation paraxiale. Le nouveau montage est celui de la figure
ci-dessous.
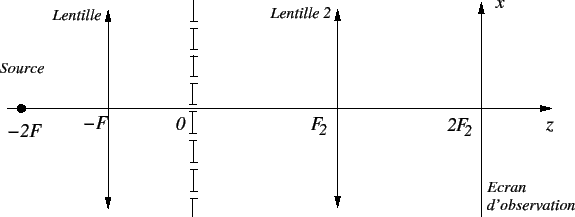
- (Question indépendante) Pourquoi dit-on que ce montage est
à double diffraction ?
- Calculer l'intensité dans le plan
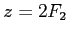
- En quel point
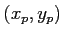 se trouve l'ordre
se trouve l'ordre 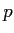 dans le plan
dans le plan 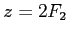 ?
?
- On limite le réseau par un diaphragme circulaire de diamètre
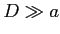 .
.
- Ecrire le nouveau coefficient de transmission du réseau.
- Ecrire l'amplitude complexe dans le plan
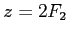
- En déduire l'intensité correspondante (on utilisera
l'hypothèse
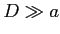 )
)
- Quelle est la largeur de la tache correspondant à l'ordre
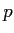 (on précisera la définition choisie pour la largeur) ?
(on précisera la définition choisie pour la largeur) ?
- Qu'appelle-t-on pouvoir de résolution du réseau ? Que vaut-il
dans l'ordre
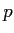 ?
?
La source est maintenant bichromatique. Elle émet de la lumière en
quantité égale à deux longueurs d'onde 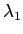 et
et 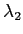 . On pose
. On pose 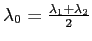 et
et 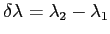 avec
avec 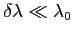 .
.
- Le réseau est de dimensions infinies. Ecrire l'intensité
lumineuse dans le plan
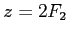 .
.
- Représenter schématiquement le graphe de l'intensité
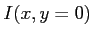 .
.
- Montrer que l'ordre
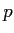 est dédoublé en deux
pics et préciser la distance entre les deux pics.
est dédoublé en deux
pics et préciser la distance entre les deux pics.
- On limite à nouveau le réseau par le diaphragme circulaire de
diamètre
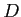 .
.
- Ecrire l'intensité dans le plan
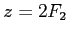
- Montrer que chaque ordre
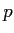 est constitué de
deux taches.
est constitué de
deux taches.
- A quelle condition sur
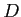 a-t-on une
superposition de ces deux taches ?
a-t-on une
superposition de ces deux taches ?
- (Question indépendante) Qu'est-ce que le critère de
Rayleigh ?
- On suppose ce critère réalisé dans l'ordre
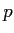 . Qu'observe-t-on alors dans les ordres
. Qu'observe-t-on alors dans les ordres 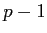 et
et 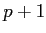 (faites un dessin)
(faites un dessin)
On s'intéresse à la propagation d'une onde plane monochromatique dans
un milieu neutre linéaire et homogène. Les champs électrique et
magnétique ont une dépendance spatio-temporelle de la forme
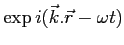 . Le milieu est caractérisé par les relations constitutives suivantes
. Le milieu est caractérisé par les relations constitutives suivantes
avec ![$ [\sigma]=\left(\begin{array}{ccc}
-i\sigma_1& \alpha &0 \\
-\alpha& -i\sigma_1 &0\\
0 &0 &i\sigma_2
\end{array}\right)$](img40.png) le tenseur de conductivité (matrice d'ordre 2), avec
le tenseur de conductivité (matrice d'ordre 2), avec 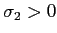 et
et 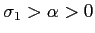 . La forme particulière de
. La forme particulière de ![$ [\sigma]$](img43.png) est dûe à la
présence d'un champ magnétique uniforme dirigé suivant
est dûe à la
présence d'un champ magnétique uniforme dirigé suivant 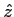 .
.
- (Question indépendante) Pourquoi ce milieu est-il
anisotrope ?
- Projeter le vecteur densité de courant
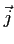 pour
obtenir les trois composantes
pour
obtenir les trois composantes 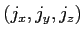 en fonction des trois composantes de
en fonction des trois composantes de 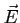
- Ecrire les équations de Maxwell dans ce milieu
- (Question indépendante) Rappeler comment s'écrivent les
opérateurs divergence et rotationnel pour une une onde plane de
dépendance
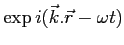 .
.
- Etablir la relation : (en cas de difficulté on pourra passer à
la suite sans traiter cette question)
![$\displaystyle k^2 \vec E-(\vec k.\vec E) \vec k=\frac{\omega^2}{c^2}\vec E+i\omega\mu_0 [\sigma]\; \vec E$](img48.png) |
(1) |
(on rappelle la formule du double produit vectoriel : 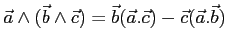 .
.
Le milieu est considéré infini dans les directions 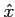 et
et 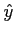 , et limité dans la tranche
, et limité dans la tranche 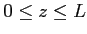 . On considère dans la suite que
. On considère dans la suite que 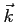 est paralèle à
est paralèle à 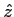 et que
et que 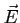 est transverse (
est transverse (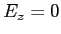 ).
).
- Projeter la relation (1) pour obtenir deux relations entre
 et
et 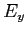
- En déduire la relation de dispersion
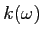 du milieu
du milieu
- (Question indépendante) Pourquoi la relation
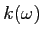 est-elle appelée ``relation de dispersion'' ?
est-elle appelée ``relation de dispersion'' ?
- (Question indépendante) quels sont les vecteurs de Jones
associés à une polarisation linéaire ? circulaire ?
- Déduire de la question 6 les états de polarisation des ondes
pouvant se propager dans le milieu
- On se place dans le cas où
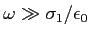 . Quelle est la vitesse de phase des ondes qui se propagent ?
. Quelle est la vitesse de phase des ondes qui se propagent ?
- En
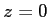 le champ électrique s'écrit
le champ électrique s'écrit 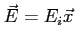 .
.
- Ecrire ce champ sous forme d'un vecteur de Jones
- En
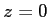 le champ transmis dans le matériau est noté
le champ transmis dans le matériau est noté 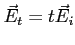 , avec
, avec 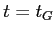 pour une onde circulaire gauche et
pour une onde circulaire gauche et 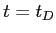 pour une onde circulaire droite. Ecrire le champ transmis
en
pour une onde circulaire droite. Ecrire le champ transmis
en 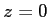
- Quel est l'état de polarisation de l'onde transmise en
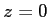 ?
?
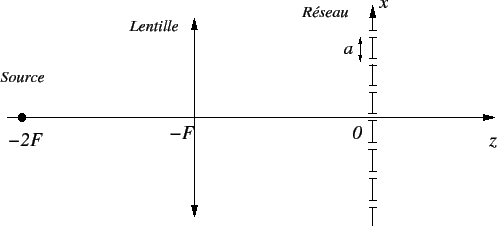
- Ecrire le champ transmis en
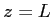 (sous forme de
vecteurs de Jones)
(sous forme de
vecteurs de Jones)
- (Question indépendante) Rappeler ce qu'est un milieu
optiquement actif
- Peut-on dire que c'est le cas ici et pourquoi ?
Voir la solution


![$ [\sigma]=\left(\begin{array}{ccc}
-i\sigma_1& \alpha &0 \\
-\alpha& -i\sigma_1 &0\\
0 &0 &i\sigma_2
\end{array}\right)$](img40.png) le tenseur de conductivité (matrice d'ordre 2), avec
le tenseur de conductivité (matrice d'ordre 2), avec ![$\displaystyle k^2 \vec E-(\vec k.\vec E) \vec k=\frac{\omega^2}{c^2}\vec E+i\omega\mu_0 [\sigma]\; \vec E$](img48.png)