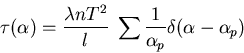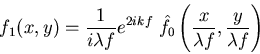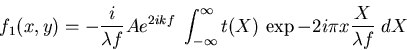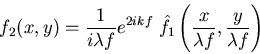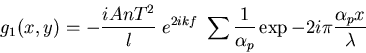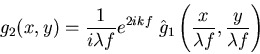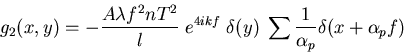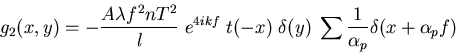- Une onde réfléchie sur la 1ère face
- Une onde qui traverse directement les deux faces
- Une onde qui traverse la face 1, se réfléchit sur la face 2, se réfléchit à nouveau sur la face 1 et traverse la face 2
- Une onde qui traverse la face 1, se réfléchit sur la face 2, puis sur la face 1 puis à nouveau sur la face 2 et sur la face 1 et traverse la face 2
- etc... jusqu'à l'infini
d'où
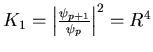 .
Et
K100=R400. Donc
.
Et
K100=R400. Donc
l'onde directement transmise s'écrit à la sortie du PF :
L'onde ``suivante'' (après deux réflexions) va s'écrire
et l'amplitude complexe à la sortie est la somme des amplitudes complexes de toutes les ondes élémentaires :
C'est une série géométrique de raison
Si R=1 alors
![]() .
L'application de la formule sommatoire de Poisson donne un peigne de Dirac
.
L'application de la formule sommatoire de Poisson donne un peigne de Dirac
l'ordre d'interférence est le nombre m de longueurs d'onde que l'on peut ``caser'' dans la différence de chemin optique
soit avec les valeurs numériques proposées :
Pour être en optique paraxiale, on considère
![]() ,
ce qui donne
,
ce qui donne ![]() .
.
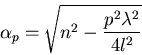
En utilisant la relation
et comme
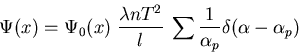
D'où le coefficient de transmission du PF