Licence de Physique LP2b -- Electromagnétisme et optique
Session de Juin 2000
Partie II -- Optique
Dans cet exercice nous allons placer un Pérot-Fabry dans le plan de filtrage d'un montage à double diffraction. Quelle est l'influence de ce Pérot-Fabry sur l'image ? C'est la question à laquelle vous allez essayer de répondre. Bonne chance !
Un Pérot-Fabry (noté PF dans la suite) est constitué de 2 lames semi-réfléchissantes identiques et parallèles emprisonnant un milieu d'indice n. La distance entre les deux lames est notée l, le coefficient de transmission en amplitude de chaque face est noté T et le coefficient de réflexion est noté R (R voisin de 1). Ce PF est éclairé sous incidence oblique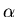 par une onde plane monochromatique cohérente de longueur d'onde
par une onde plane monochromatique cohérente de longueur d'onde 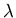 et d'amplitude
et d'amplitude 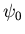 .
.
- 1.
- Expliquer pourquoi l'on observe à la sortie du PF une infinité d'ondes planes. Dans quelles directions se propagent-elles ? Ces ondes interfèrent-elles entre elles ? On rappelle (cf. TP) que le déphasage
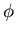 entre deux ondes successives (numérotées p et p+1) à la sortie du PF vaut
entre deux ondes successives (numérotées p et p+1) à la sortie du PF vaut
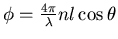 ,
,
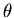 étant l'angle réfracté sur la face d'entrée (
étant l'angle réfracté sur la face d'entrée (
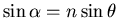 ).
).
- 2.
- (Question facultative) Quel est le rapport des intensités K1 entre les ondes p et p+1 ? Quelle valeur minimale doit avoir R pour que le rapport d'intensité K100 entre les ondes p et p+100 soit supérieur à 10 % ?
- 3.
- Ecrire sous forme d'une série géométrique l'amplitude à la sortie du PF en fonction de la variable
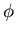 .
Dans le cas où
.
Dans le cas où
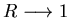 montrer qu'elle tend vers un peigne de Dirac. Dans la suite on supposera R=1.
montrer qu'elle tend vers un peigne de Dirac. Dans la suite on supposera R=1.
- 4.
- Quelles sont les valeurs de
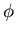 pour lesquelles l'amplitude sortante n'est pas nulle ? En déduire les valeurs d'incidence
pour lesquelles l'amplitude sortante n'est pas nulle ? En déduire les valeurs d'incidence 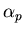 pour lesquelles la lumière est transmise par le PF. A quels ordres d'interférence correspondent-elles ?
pour lesquelles la lumière est transmise par le PF. A quels ordres d'interférence correspondent-elles ?
- 5.
- (Question facultative) Quel est l'ordre d'interférence maximal observable ? Pour quels ordres d'interférence est-on en optique paraxiale (on considèrera qu'on est en optique paraxiale si
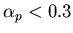 ) ? A.N.: l=0.1 mm,
) ? A.N.: l=0.1 mm,
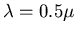 m, n=1.5.
m, n=1.5.
- 6.
- Ecrire
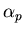 dans l'approximation paraxiale. Calculer, en fonction de l'incidence
dans l'approximation paraxiale. Calculer, en fonction de l'incidence 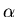 et de
et de 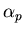 ,
le coefficient de transmission
,
le coefficient de transmission
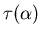 du PF (rapport des amplitudes sortante et entrante). On rappelle que
du PF (rapport des amplitudes sortante et entrante). On rappelle que
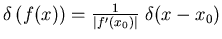 pour une fonction f s'annulant en x0.
pour une fonction f s'annulant en x0.
Les questions 1,2 et 3 sont indépendantes de l'exercice précédent.
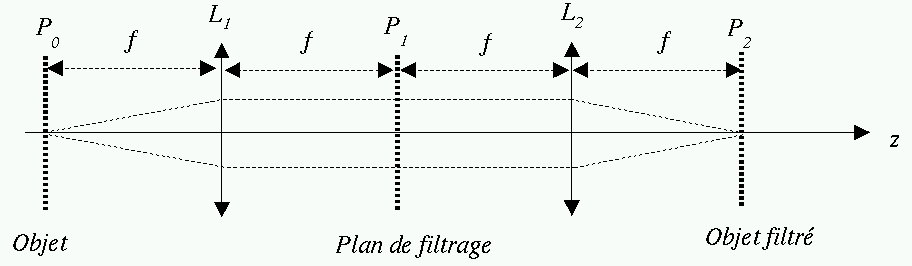
On considère le montage à deux lentilles de la figure ci-dessous. Les deux lentilles sont identiques, de focales f. La distance qui les sépare est 2f(foyers conjugués). Un objet de coefficient de transmission
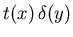 (infiniment fin dans la direction y) est placé dans le plan P0 à une distance f en amont de la première lentille, il est éclairé sous incidence normale par une onde plane monochromatique de longueur d'onde
(infiniment fin dans la direction y) est placé dans le plan P0 à une distance f en amont de la première lentille, il est éclairé sous incidence normale par une onde plane monochromatique de longueur d'onde 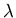 et d'amplitude A dans le plan P0. On se place dans l'approximation paraxiale.
et d'amplitude A dans le plan P0. On se place dans l'approximation paraxiale.
>
- 1.
- Ecrire l'amplitude complexe dans le plan P1. Montrer que cette amplitude complexe est une somme d'ondes planes se propageant dans toutes les directions du plan (xz). Quelles sont les amplitudes associées à ces ondes planes ?
- 2.
- Ecrire l'amplitude complexe dans le plan P2, plan focal image de la seconde lentille. Comparer les amplitudes dans les plans P0 et P2.
- 3.
- On suppose que t(x)=1. Quelle est alors la nature de l'onde entre les plans de l'objet et de la première lentille (aucun calcul n'est demandé) ?
- 4.
- On place le PF de l'exercice précédent dans le plan P1. En introduisant le coefficient de transmission
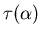 du PF, écrivez l'amplitude complexe à la sortie du PF (le plus commode est d'écrire ces amplitudes complexes comme des sommes d'ondes planes). Montrez que c'est une somme discrète d'ondes planes.
du PF, écrivez l'amplitude complexe à la sortie du PF (le plus commode est d'écrire ces amplitudes complexes comme des sommes d'ondes planes). Montrez que c'est une somme discrète d'ondes planes.
- 5.
- Ecrire l'amplitude complexe dans le plan P2. Décrire la figure observée. Faire un dessin détaillé.
- 6.
- Même question pour t(x) quelconque. Montrez que la présence du PF dans le plan de filtrage permet de réaliser un échantillonage de l'objet. Quel est le pas d'échantillonnage ?
- 7.
- Dans le cas où t(x,y) est un diaphragme circulaire placé dans le plan P0, expliquez sans calcul l'observation de cercles concentriques brillants dans l'image en P2. Quels sont les rayons de ces cercles ?
Voir la solution
![]() (infiniment fin dans la direction y) est placé dans le plan P0 à une distance f en amont de la première lentille, il est éclairé sous incidence normale par une onde plane monochromatique de longueur d'onde
(infiniment fin dans la direction y) est placé dans le plan P0 à une distance f en amont de la première lentille, il est éclairé sous incidence normale par une onde plane monochromatique de longueur d'onde ![]() et d'amplitude A dans le plan P0. On se place dans l'approximation paraxiale.
et d'amplitude A dans le plan P0. On se place dans l'approximation paraxiale.
