Licence de Physique LP2b -- Electromagnétisme et optique
Session de Juin 2001
Partie II -- Optique
Dans tout le problème, on suppose réalisées
les conditions de Gauss (petits angles). Ca parait long mais il y a très
peu de calculs ; soignez la rédaction et la clarté des explications,
ne négligez pas de vérifier que vos résultats sont
homogènes, n'hésitez pas à faire des schémas...
1. Une lentille éclairée
par une onde plane

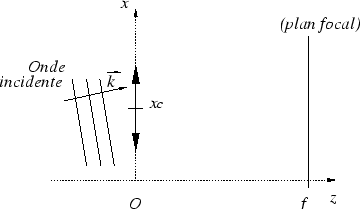
-
Faire un dessin de l'intensité au foyer de la lentille (le calcul
n'est pas demandé)
-
Donner la position
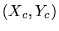 du centre de la tache observée au foyer .
du centre de la tache observée au foyer .
-
Quelle est la taille de cette tache ? (A.N. :
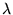 =500
nm,
=500
nm, 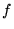 =5
cm,
=5
cm, 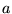 =25
mm)
=25
mm)
-
Quelle est la pente
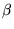 que fait le front d'onde avec le plan
que fait le front d'onde avec le plan 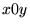 ? Si cette pente varie d'une petite quantité d
? Si cette pente varie d'une petite quantité d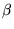 ,
de quelle valeur d
,
de quelle valeur d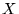 se déplace la tache au foyer de la lentille ?
se déplace la tache au foyer de la lentille ?
-
On suppose que le plus petit déplacement mesurable de
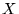 est d'un dixième de la taille de la tache focale ; quelle est alors
la plus petite variation de la pente du front d'onde d
est d'un dixième de la taille de la tache focale ; quelle est alors
la plus petite variation de la pente du front d'onde d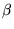 que l'on peut mesurer ? (A.N.: mêmes valeurs que la question précédente).
que l'on peut mesurer ? (A.N.: mêmes valeurs que la question précédente).
2. La lentille est éclairée
par une onde non plane
Une onde plane monochromatique de longueur d'onde 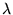 se propageant dans la direction
se propageant dans la direction 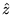 éclaire une lame d'épaisseur fixe
éclaire une lame d'épaisseur fixe 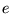 qui possède un indice variable
qui possède un indice variable 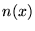 .
Juste après la traversée de la lame, l'onde arrive sur la
lentille de la question précédente.
.
Juste après la traversée de la lame, l'onde arrive sur la
lentille de la question précédente.
-
Ecrire l'amplitude complexe de l'onde à la sortie de la lame.
-
Quelle est la nature de l'onde dans les cas suivants :
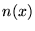 constant ;
constant ; 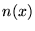 linéraire ;
linéraire ; 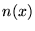 quadratique ;
quadratique ; 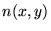 quadratique en
quadratique en 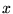 et
et 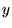
-
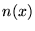 est cette fois quelconque mais lentement variable devant le diamètre
de la lentille (en d'autres termes : sur la lentille,
est cette fois quelconque mais lentement variable devant le diamètre
de la lentille (en d'autres termes : sur la lentille, 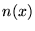 s'identifie à son développement au premier ordre autour du
centre de la lentille). Quelle est la pente locale
s'identifie à son développement au premier ordre autour du
centre de la lentille). Quelle est la pente locale 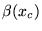 du front d'onde au centre de la lentille ? Relier cette pente locale à
la position de la tache image au foyer de la lentille.
du front d'onde au centre de la lentille ? Relier cette pente locale à
la position de la tache image au foyer de la lentille.
-
Sachant que la mesure de la position de la tache focale se fait avec une
précision d'un dixième de la taille de la tache, quelle est
la plus petite valeur de
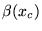 mesurable ? Quelle est donc la plus petite valeur mesurable de la dérivée
de l'indice en
mesurable ? Quelle est donc la plus petite valeur mesurable de la dérivée
de l'indice en 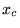 ? (A.N. mêmes valeurs avec
? (A.N. mêmes valeurs avec 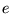 =1
mm).
=1
mm).
3. Analyseur de front d'onde
de Shack-Hartmann

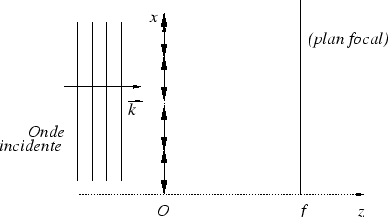
-
Même question si l'onde incidente est sous incidence oblique (
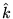 de composantes
de composantes 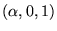 ).
).
-
L'incidence est à nouveau normale, mais on insère juste avant
le réseau de lentilles la lame d'indice variable
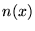 de la question précédente. Ecrire la position
de la question précédente. Ecrire la position 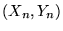 de la tache focale de la lentille numéro
de la tache focale de la lentille numéro  en fonction de la pente locale
en fonction de la pente locale 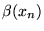 du front d'onde au centre de la lentille.
du front d'onde au centre de la lentille.
-
A partir de la mesure de la pente du front d'onde au centre de chaque lentille,
et en supposant que
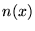 est une fonction continue, montrer graphiquement comment on peut obtenir
grossièrement, et à une constante près, la forme du
front d'onde à l'entrée du réseau de lentilles
est une fonction continue, montrer graphiquement comment on peut obtenir
grossièrement, et à une constante près, la forme du
front d'onde à l'entrée du réseau de lentilles
Ce système de mesure des pentes locales du front d'onde à
réseau de micro-lentilles est appelé ``analyseur de front
d'onde de Shack-Hartmann''. Il est utilisé dans les grands télescopes
équipés d'optique adaptative (par exemple les 4 télescopes
du VLT au Chili) pour corriger les déformations de front d'onde
induites par la turbulence atmosphérique.
Voir la solution



