Licence de Physique LP2b -- Electromagnétisme et optique
Session de Juin 2002
Partie II -- Optique
Les 3 exercices sont indépendants. N'oubliez pas de tourner
la page.
Diffraction
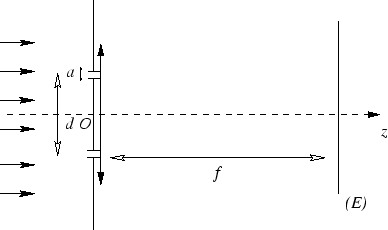
Un masque percé de deux trous carrés de côté 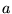 est accolé à une lentille mince convergente de focale
est accolé à une lentille mince convergente de focale 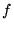 .
La distance entre les deux trous du masque est
.
La distance entre les deux trous du masque est 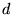 (avec
(avec 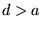 ).
Cet ensemble est éclairé sous incidence normale par une onde
plane de longueur d'onde
).
Cet ensemble est éclairé sous incidence normale par une onde
plane de longueur d'onde 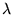 et d'amplitude
et d'amplitude 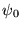 dans le plan du masque.
dans le plan du masque.
-
Ecrire l'amplitude complexe juste avant la traversée de la lentille
puis au foyer de celle-ci.
-
Faire un schéma de l'intensité au foyer, donner un ordre
de grandeur du nombre de franges visibles en fonction du rapport
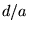 .
.
-
On place sur l'un des trous un prisme d'angle au sommet
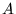 et d'indice
et d'indice 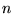 .
Que se passe-t'il ? Que représente la quantité
.
Que se passe-t'il ? Que représente la quantité 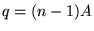 ? Décrire l'intensité au foyer lorsque
? Décrire l'intensité au foyer lorsque 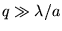 et lorsque
et lorsque 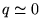 .
D'après-vous(et sans calcul), quelle est l'allure de l'image lorsque
.
D'après-vous(et sans calcul), quelle est l'allure de l'image lorsque 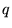 est inférieur et de l'ordre de
est inférieur et de l'ordre de 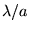 (par exemple
(par exemple  )
?
)
?
-
On enlève le prisme. Quelle est l'intensité au foyer si les
deux trous sont éclairés par des ondes planes
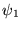 et
et 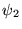 provenant de sources différentes (par exemple deux lasers, chacun
éclairant l'un des trous) ?).
provenant de sources différentes (par exemple deux lasers, chacun
éclairant l'un des trous) ?).
Voir la solution
Cohérence spatiale
-
Calculer la largeur de cohérence spatiale du Soleil à 21
cm de longueur d'onde (raie d'émission l'hydrogène neutre
dûe au changement de spin de l'électron). Le diamètre
angulaire du soleil est 1/2 degré.
-
Deux antennes situées à 5 m d'une de l'autre observent le
Soleil à 21 cm de longueur d'onde ; on fait interférer les
deux ondes. Observera-t'on des franges interférences ? Même
question si les antennes sont distantes de 100 m.
Spectroscope
Le spectrographe de la lunette Coudée de l'observatoire de Nice
peut être schématisé comme suit :
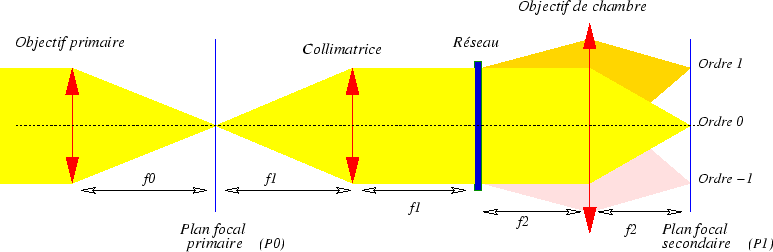
L'objectif principal est celui de la lunette coudée. C'est une
lentille de 40 cm de diamètre et de focale 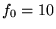 mètres. Elle forme une image en son plan focal (plan
mètres. Elle forme une image en son plan focal (plan 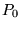 ).
La lentille suivante (collimatrice) a une focale
).
La lentille suivante (collimatrice) a une focale 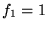 m, son plan focal objet est confondu avec le plan focal primaire
m, son plan focal objet est confondu avec le plan focal primaire 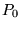 .
Le réseau est un carré de 5 cm de largeur sur lequel sont
gravés 600 traits par mm. Il est placé au plan focal image
de la lentille collimatrice. La dernière lentille (dite de chambre)
a une focale
.
Le réseau est un carré de 5 cm de largeur sur lequel sont
gravés 600 traits par mm. Il est placé au plan focal image
de la lentille collimatrice. La dernière lentille (dite de chambre)
a une focale 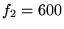 mm. Son plan focal objet est situé au niveau du réseau, le
plan focal image dans lequel on observe le spectre des étoiles est
mm. Son plan focal objet est situé au niveau du réseau, le
plan focal image dans lequel on observe le spectre des étoiles est 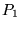 .
On suppose que les dimensions transversales des lentilles collimatrice
et de chambre sont infinies.
.
On suppose que les dimensions transversales des lentilles collimatrice
et de chambre sont infinies.
On se place dans les conditions de l'optique paraxiale.
-
On suppose dans un premier temps que l'onde incidente est plane, monochromatique
de longueur d'onde
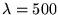 nm et que l'incidence est normale. Décrire l'image (intensité)
au plan focal primaire
nm et que l'incidence est normale. Décrire l'image (intensité)
au plan focal primaire 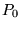 (faire un dessin annoté). Quelle est la taille de l'image ?
(faire un dessin annoté). Quelle est la taille de l'image ?
-
On suppose dans la suite que les dimensions transversales de l'objectif
principal sont infinies. Comment s'écrit alors l'amplitude complexe
dans le plan
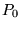 ? Montrez que l'onde est plane en arrivant sur le réseau.
? Montrez que l'onde est plane en arrivant sur le réseau.
-
Donner les directions dans lesquelles se propagent les différents
ordres en sortie du réseau. Quel est l'ordre maximal observable
?
-
On s'intéresse à l'ordre zéro seul. Ecrire l'intensité
dans le plan du réseau puis dans le plan
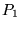 .
Quelle est la taille de l'image (le réseau est un carré de
5 cm de largeur) ?
.
Quelle est la taille de l'image (le réseau est un carré de
5 cm de largeur) ?
-
Même question en tenant compte de l'ensemble des ordres diffractés
par le réseau. Quelle est la distance entre les taches formées
par les différents ordres ? Combien y-a t'il d'ordres observables
?
Voir la solution



![]() mètres. Elle forme une image en son plan focal (plan
mètres. Elle forme une image en son plan focal (plan ![]() ).
La lentille suivante (collimatrice) a une focale
).
La lentille suivante (collimatrice) a une focale ![]() m, son plan focal objet est confondu avec le plan focal primaire
m, son plan focal objet est confondu avec le plan focal primaire ![]() .
Le réseau est un carré de 5 cm de largeur sur lequel sont
gravés 600 traits par mm. Il est placé au plan focal image
de la lentille collimatrice. La dernière lentille (dite de chambre)
a une focale
.
Le réseau est un carré de 5 cm de largeur sur lequel sont
gravés 600 traits par mm. Il est placé au plan focal image
de la lentille collimatrice. La dernière lentille (dite de chambre)
a une focale ![]() mm. Son plan focal objet est situé au niveau du réseau, le
plan focal image dans lequel on observe le spectre des étoiles est
mm. Son plan focal objet est situé au niveau du réseau, le
plan focal image dans lequel on observe le spectre des étoiles est ![]() .
On suppose que les dimensions transversales des lentilles collimatrice
et de chambre sont infinies.
.
On suppose que les dimensions transversales des lentilles collimatrice
et de chambre sont infinies.