Licence de Physique LP2b -- Electromagnétisme et
optique
Session de Juin 2003
Optique
Merci de rédiger les examens d'optique et d'electromagnétisme
sur des copies séparées.
On réalise une expérience d'interférences en éclairant
un dispositif de trous d'Young avec une onde plane polychromatique arrivant
sous incidence normale. La distance entre les deux trous, alignés
le long de l'axe 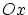 est
est 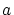 , les franges sont observées
sur un écran
, les franges sont observées
sur un écran 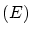 placé à une distance
placé à une distance
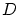 du plan des trous. On suppose que
du plan des trous. On suppose que 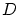 est assez
grand pour pouvoir faire l'approximation de la diffraction à l'infini.
On appelle
est assez
grand pour pouvoir faire l'approximation de la diffraction à l'infini.
On appelle 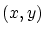 les coordonnées d'un point
les coordonnées d'un point 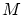 de
de 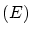 où l'on observe les franges d'interférences.
où l'on observe les franges d'interférences.
Le spectre de la lumière est de la forme
où 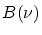 est le spectre de la lumière blanche,
modélisé par une gaussienne de largeur
est le spectre de la lumière blanche,
modélisé par une gaussienne de largeur 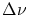 centrée sur la fréquence
centrée sur la fréquence 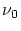 .
.
- Dessiner grossièrement le spectre de l'onde incidente lorsque
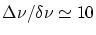 . Pourquoi parle-t'on de spectre cannelé ?
Quel est l'ordre de grandeur du nombre de cannelures dans
. Pourquoi parle-t'on de spectre cannelé ?
Quel est l'ordre de grandeur du nombre de cannelures dans  ?
?
- Calculer la transformée de Fourier
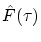 .
.
- Calculer l'intensité qui serait observée dans le plan
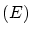 si la lumière incidente était monochromatique
(fréquence
si la lumière incidente était monochromatique
(fréquence 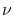 ).
).
- En déduire l'intensité des franges d'interférences
au point
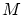 si le spectre de la lumière incidente est
si le spectre de la lumière incidente est
 (on considère que
(on considère que
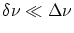 ).
).
- Dessiner l'aspect du champ d'interférences lorsque
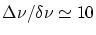 . Montrer qu'on observe
dans ce cas trois paquets de franges centrées en
. Montrer qu'on observe
dans ce cas trois paquets de franges centrées en 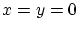 et
et
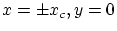 , calculer
, calculer
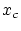 .
.
- Combien observe-t'on de franges dans chaque paquet ? A.N : le
spectre
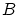 de la lumière blanche est centré
sur la longueur d'onde 500 nm avec une largeur de 100 nm. Quelle
condition doit-on remplir pour qu'il n'y ait pas de recouvrement entre les
trois paquets ?
de la lumière blanche est centré
sur la longueur d'onde 500 nm avec une largeur de 100 nm. Quelle
condition doit-on remplir pour qu'il n'y ait pas de recouvrement entre les
trois paquets ?
Voir la solution
On considère un écran opaque de dimension transversales infinies
percé de trois trous carrés de côté 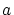 répartis sur les sommets d'un triangle équilatéral
de côté
répartis sur les sommets d'un triangle équilatéral
de côté 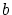 (voir schéma ci-dessous).
L'ensemble est éclairé sous incidence normale par une onde
plane monochromatique de longueur d'onde
(voir schéma ci-dessous).
L'ensemble est éclairé sous incidence normale par une onde
plane monochromatique de longueur d'onde 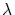 et d'amplitude
et d'amplitude
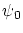 dans le plan du masque.
dans le plan du masque.
- Ecrire le coefficient de transmission du masque.
- Ecrire l'intensité diffractée
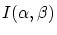 à l'infini dans la direction
du vecteur unitaire
à l'infini dans la direction
du vecteur unitaire 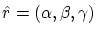 .
.
- Mettre en évidence la présence dans l'intensité
de trois système de franges d'Young superposées. On précisera
les écartements (vecteurs) des trois paires de trous correspondantes.
Etes-vous étonnés par ce résultat (et pourquoi) ?
- Dessiner l'aspect du champ d'interférences et tracez le graphe
de l'intensité
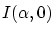 puis de
puis de 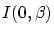 . Les graphes doivent comprendre les annotations d'usage.
. Les graphes doivent comprendre les annotations d'usage.
- On désire obtenir une intensité nulle (donc une amplitude
nulle) au centre de la figure de diffraction à l'infini. Pour ce faire
on place sur les trous des lames cristallines permettant d'introduire un
déphasage sur l'amplitude. Combien de lames doit-on utiliser, quels
déphasages doit-on introduire et comment doit-on les disposer pour
obtenir ce résultat ?
Voir la solution
![]() est
est ![]() , les franges sont observées
sur un écran
, les franges sont observées
sur un écran ![]() placé à une distance
placé à une distance
![]() du plan des trous. On suppose que
du plan des trous. On suppose que ![]() est assez
grand pour pouvoir faire l'approximation de la diffraction à l'infini.
On appelle
est assez
grand pour pouvoir faire l'approximation de la diffraction à l'infini.
On appelle ![]() les coordonnées d'un point
les coordonnées d'un point ![]() de
de ![]() où l'on observe les franges d'interférences.
où l'on observe les franges d'interférences.