Licence de Physique LP2b -- Electromagnétisme et
optique
Session de Juin 2004
Optique
Merci de rédiger les examens d'optique et d'electromagnétisme
sur des copies séparées.
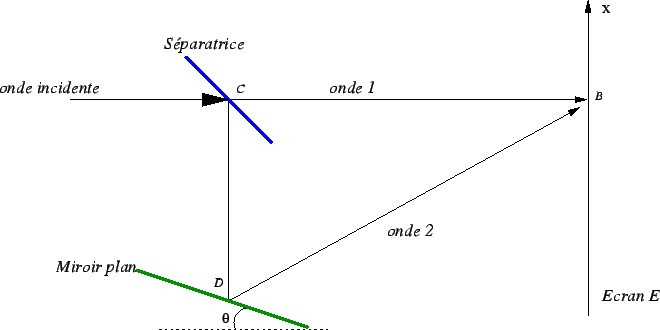
Soit le montage optique de la figure ci-après. Il est composé
d'une lame séparatrice qui divise le faisceau de lumière incidente
en deux parties égales. L'une de ces parties éclaire un écran
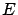 . L'autre partie est renvoyée vers un miroir plan incliné
de l'angle
. L'autre partie est renvoyée vers un miroir plan incliné
de l'angle 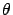 indiqué sur la figure avant de venir
à son tour éclairer l'écran
indiqué sur la figure avant de venir
à son tour éclairer l'écran 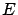 (
(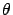 n'est pas forcément un petit angle). On appelle
n'est pas forcément un petit angle). On appelle 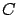 le centre de la séparatrice,
le centre de la séparatrice, 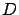 le centre
du miroir plan et
le centre
du miroir plan et 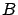 le centre de l'écran
le centre de l'écran 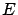 . On pourra
noter
. On pourra
noter 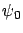 l'amplitude de l'onde incidente.
l'amplitude de l'onde incidente.
Les distances sont 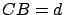 ,
, 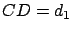 et
et 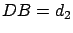 .
.
- L'éclairage est monochromatique et sous incidence normale (vecteur
d'onde parallèle à la droite
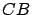 ).
).
- Ecrire l'intensité des franges d'interférences dans
le plan
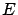 . On pourra s'aider d'un schéma équivalent
pour la propagation de l'onde 2.
. On pourra s'aider d'un schéma équivalent
pour la propagation de l'onde 2.
- Quel est le contraste des franges et l'interfrange ?
- Montrer que la figure d'interférences est affectée
d'un décalage d'origine
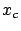 . Que vaut
. Que vaut 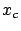 ?
?
- Le spectre de la lumière est celui de la lumière blanche,
modélisé par une gaussienne de largeur
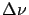 centrée sur
centrée sur 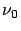 Ce spectre s'écrit
Ce spectre s'écrit
- A partir du résultat de la quetsion 1, écrire l'intensité
des franges dans le plan
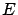
- Ecrire et représenter la fonction
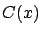 donnant
le contraste des franges en un point de l'écran
donnant
le contraste des franges en un point de l'écran 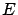 .
.
- Représenter l'intensité des franges pour
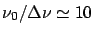 .
.
Voir la solution
Une grille bidimensionnelle de points a pour coefficient de transmission
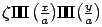 avec
avec 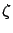 et
et 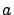 des constantes réelles
positives et
des constantes réelles
positives et  désigne le peigne de Dirac.
Cette grille est limitée spatialement par un diaphragme carré
de coté
désigne le peigne de Dirac.
Cette grille est limitée spatialement par un diaphragme carré
de coté 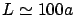 . L'ensemble est appelé ``masque''
dans la suite.
. L'ensemble est appelé ``masque''
dans la suite.
- Quelle est la dimension de
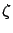 (argumentez) ?
(argumentez) ?
- Quel est le pouvoir de résolution de ce réseau dans l'ordre
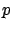 si la longueur d'onde est
si la longueur d'onde est 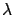 ?
A quel(s) ordre(s) peut-on résoudre le doublet du Sodium (longueurs
d'ondes 5890 et 5896 Å) ?
?
A quel(s) ordre(s) peut-on résoudre le doublet du Sodium (longueurs
d'ondes 5890 et 5896 Å) ?
- Le masque est placé dans le plan focal objet d'une lentille
convergente de focale
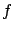 . On éclaire en lumière
monochromatique (onde plane) sous incidence normale. Décrire l'image
dans le plan focal image de la lentille et faire un dessin annoté
(
. On éclaire en lumière
monochromatique (onde plane) sous incidence normale. Décrire l'image
dans le plan focal image de la lentille et faire un dessin annoté
(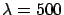 nm,
nm, 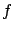 =20 cm,
=20 cm, 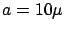 m).
m).
- Même question mais l'éclairage se fait avec deux longueurs
d'onde (celles du doublet du Sodium). Il ne sera pas nécessaire d'écrire
explicitement l'intensité. Un raisonnement qualitatif à partir
du résultat de la question précédente suffit.
- (Question indépendante de la précédente)
On revient à l'éclairage monochromatique (
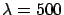 nm). On place au centre du plan focal image de
la lentille un diaphragme circulaire de rayon 2 mm. Une seconde lentille
identique à la première permet d'observer l'objet filtré
par ce trou. Dessiner le montage optique qui permet cette observation. Calculer
l'intensité de l'objet filtré (on fera les approximations correspondant
aux valeurs numériques en jeu dans le problème).
nm). On place au centre du plan focal image de
la lentille un diaphragme circulaire de rayon 2 mm. Une seconde lentille
identique à la première permet d'observer l'objet filtré
par ce trou. Dessiner le montage optique qui permet cette observation. Calculer
l'intensité de l'objet filtré (on fera les approximations correspondant
aux valeurs numériques en jeu dans le problème).
Voir la solution


![]() ,
, ![]() et
et ![]() .
. 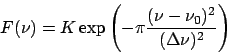
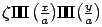 avec
avec