L3 Physique -- Premier partiel d'optique
5 Mars 2014
2 pages, durée 1h30
Documents autorisés : une feuille A4 recto-verso manuscrite, formulaire de TF.
- Rappeler ce que doit être la dimension (quelle unité) d'un coefficient de transmission
- Ecrire coefficient de transmission d'un diaphragme carré de côté
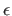 (on appellera
(on appellera 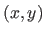 les coordonnées d'un point dans le plan du diaphragme).
les coordonnées d'un point dans le plan du diaphragme).
- On fait tendre
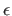 vers 0 de sorte que le diaphragme devienne un trou quasi-ponctuel. Vers quelle quantité, fonction de
vers 0 de sorte que le diaphragme devienne un trou quasi-ponctuel. Vers quelle quantité, fonction de 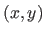 tend le coefficient de transmission ?
tend le coefficient de transmission ?
- Dans cette hypothèse, calculer l'intensité diffractée à l'infini par ce trou lorsqu'il est éclairé sous incidence normale par une onde plane de longueur d'onde
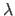 et d'amplitude constante
et d'amplitude constante 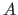 dans le plan du trou.
dans le plan du trou.

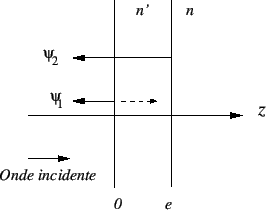
Le principe de la couche anti-reflets consiste à déposer sur le dioptre, une couche très mince d'un produit transparent d'indice 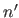 inférieur à l'indice
inférieur à l'indice 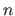 du verre. On crée ainsi deux ondes réfléchies qui s'annulent par interférence destructrice si l'épaisseur et l'indice de la couche sont bien choisis.
du verre. On crée ainsi deux ondes réfléchies qui s'annulent par interférence destructrice si l'épaisseur et l'indice de la couche sont bien choisis.
On considère une onde plane de longueur d'onde 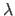 se propageant dans l'air parallèlement à l'axe
se propageant dans l'air parallèlement à l'axe 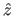 et dans le sens des
et dans le sens des 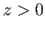 . Son amplitude complexe vaut
. Son amplitude complexe vaut 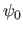 dans le plan
dans le plan 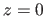 . Cette onde rencontre la couche anti-reflets d'indice
. Cette onde rencontre la couche anti-reflets d'indice 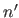 dans le plan
dans le plan 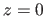 et se sépare en une onde réfléchie
et se sépare en une onde réfléchie 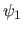 et une onde transmise. Cette onde transmise rencontre le verre d'indice
et une onde transmise. Cette onde transmise rencontre le verre d'indice 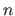 dans le plan
dans le plan 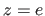 et donne naissance à une seconde onde réfléchie
et donne naissance à une seconde onde réfléchie 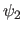 .
.
Compte-tenu des valeurs habituelles des indices des verres et des couches, il sera inutile de prendre en compte les réflexions multiples dans la couche anti-reflet. De même, on approximera les coefficients de transmission à 1. L'indice de l'air sera pris égal à 1.
- Ecrire l'amplitude complexe
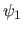 de la première onde réfléchie à la sortie de la couche anti-reflets en
de la première onde réfléchie à la sortie de la couche anti-reflets en 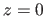 .
.
- Ecrire l'amplitude complexe
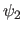 de la seconde onde réfléchie à la sortie de la couche anti-reflets en
de la seconde onde réfléchie à la sortie de la couche anti-reflets en 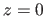 . On pourra utiliser un schéma équivalent plus simple pour la propagation de cette onde.
. On pourra utiliser un schéma équivalent plus simple pour la propagation de cette onde.
- A quelle condition sur
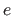 a-t-on une opposition de phase entre
a-t-on une opposition de phase entre 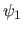 et
et 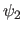 , c'est à dire que le rapport
, c'est à dire que le rapport 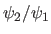 est un réel négatif (on rappelle que
est un réel négatif (on rappelle que 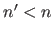 ) ?
) ?
- En supposant cette condition réalisée, quelle est la valeur de
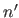 qui annule la somme
qui annule la somme 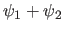 ?
?
On considère une source ponctuelle dans le vide, située en un point de coordonnées 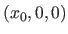 avec
avec 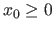 . Cette source émet une onde sphérique de longueur d'onde
. Cette source émet une onde sphérique de longueur d'onde 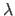 . Dans le plan
. Dans le plan 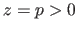 se trouve une lentille convergente de focale
se trouve une lentille convergente de focale 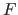 . On se place dans les conditions de l'optique paraxiale.
. On se place dans les conditions de l'optique paraxiale.
- Ecrire le coefficient de transmission de la lentille en fonction des coordonnées
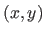
- Ecrire l'amplitude complexe à la sortie de la lentille (plan
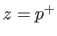 ) lorsque
) lorsque 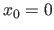 et
et 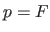 . Décrire cette onde (quel type d'onde, quelle direction de propagation, etc...), faire éventuellement un dessin.
. Décrire cette onde (quel type d'onde, quelle direction de propagation, etc...), faire éventuellement un dessin.
- On suppose
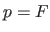 et
et 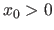 .
.
- A quelle condition sur
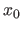 peut-on faire l'approximation paraxiale (aucune démonstration n'est demandée) ?
peut-on faire l'approximation paraxiale (aucune démonstration n'est demandée) ?
- Ecrire l'amplitude complexe à la sortie de la lentille (plan
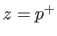 ). Décrire cette onde (quel type d'onde, quelle direction de propagation, etc...), faire éventuellement un dessin.
). Décrire cette onde (quel type d'onde, quelle direction de propagation, etc...), faire éventuellement un dessin.
- On suppose
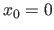 et
et 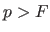 .
.
- Ecrire l'amplitude complexe à la sortie de la lentille (plan
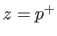 )
)
- A quoi voit-on que l'on a affaire à une onde sphérique ?
- Est-elle convergente ou divergente ?
- Identifier la position
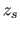 du centre de cette onde (sa source si l'onde est divergente ou son point de convergence si l'onde est convergente).
du centre de cette onde (sa source si l'onde est divergente ou son point de convergence si l'onde est convergente).
- On appelle
 la quantité
la quantité 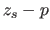 . Relier
. Relier  à
à 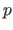 et
et 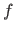 et montrer qu'on retrouve la formule de conjugaison de l'optique géométrique.
et montrer qu'on retrouve la formule de conjugaison de l'optique géométrique.
Voir la solution


![]() inférieur à l'indice
inférieur à l'indice ![]() du verre. On crée ainsi deux ondes réfléchies qui s'annulent par interférence destructrice si l'épaisseur et l'indice de la couche sont bien choisis.
du verre. On crée ainsi deux ondes réfléchies qui s'annulent par interférence destructrice si l'épaisseur et l'indice de la couche sont bien choisis.
![]() se propageant dans l'air parallèlement à l'axe
se propageant dans l'air parallèlement à l'axe ![]() et dans le sens des
et dans le sens des ![]() . Son amplitude complexe vaut
. Son amplitude complexe vaut ![]() dans le plan
dans le plan ![]() . Cette onde rencontre la couche anti-reflets d'indice
. Cette onde rencontre la couche anti-reflets d'indice ![]() dans le plan
dans le plan ![]() et se sépare en une onde réfléchie
et se sépare en une onde réfléchie ![]() et une onde transmise. Cette onde transmise rencontre le verre d'indice
et une onde transmise. Cette onde transmise rencontre le verre d'indice ![]() dans le plan
dans le plan ![]() et donne naissance à une seconde onde réfléchie
et donne naissance à une seconde onde réfléchie ![]() .
.