Licence de Physique -- Premier partiel d'optique II
Documents: feuille A4 RV manuscrite + formulaire de TF - durée 2h
Date: 14 Novembre 2008
On considère un réseau dont le coefficient de transmission vaut alternativement 0 ou 1 sur des plages de largeur 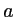 comme dessiné sur la
figure ci-contre. Ce réseau, supposé infini pour l'instant, est éclairé sous incidence normale par une onde plane monochromatique de longueur d'onde
comme dessiné sur la
figure ci-contre. Ce réseau, supposé infini pour l'instant, est éclairé sous incidence normale par une onde plane monochromatique de longueur d'onde 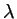 et d'amplitude
et d'amplitude 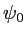 dans le plan du réseau.
dans le plan du réseau.
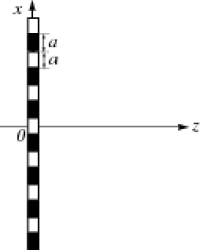
- Donner la période de ce réseau. Ecrire son coefficient de transmission
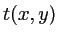
- Question indépendante des suivantes : Montrer qu'à la sortie, on a une superposition d'ondes planes se propageant dans des directions caractérisées par des vecteurs unitaires de composantes
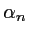 sur l'axe
sur l'axe 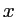 que l'on calculera, et pondérées par des coefficients que l'on explicitera.
que l'on calculera, et pondérées par des coefficients que l'on explicitera.
- Calculer la figure de diffraction à l'infini (intensité
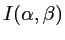 dans une direction
dans une direction
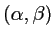 ) de ce réseau.
) de ce réseau.
- Expliquer pourquoi les ordres pairs (correspondants à
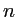 pair non nul) sont absents.
pair non nul) sont absents.
- Tracer le graphe de
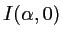
- Quel est l'ordre maximal observable si
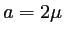 m et
m et
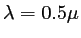 m ? Combien voit-on alors de pics dans l'intensité
m ? Combien voit-on alors de pics dans l'intensité
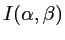 ?
?
- Comment l'intensité est-elle modifiée si la largeur des plages noires vaut
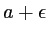 et celle des plages blanches
et celle des plages blanches
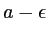 ?
?
- Les plages blanches et noires sont à nouveau de largeur
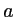 . Comment l'intensité est-elle modifiée si on suppose que le réseau est tronqué par une porte de largeur
. Comment l'intensité est-elle modifiée si on suppose que le réseau est tronqué par une porte de largeur 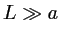 dans la direction
dans la direction  ? Quel est dans ce cas le pouvoir de résolution du réseau dans l'ordre
? Quel est dans ce cas le pouvoir de résolution du réseau dans l'ordre 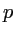 ?
?
On réalise le montage à double diffraction ci-après à l'aide de deux lentilles convergentes, 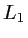 de focale
de focale 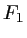 et
et 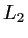 de focale
de focale  . On note
. On note 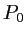 le plan focal objet de la première lentille,
le plan focal objet de la première lentille, 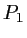 son plan focal image confondu avec le plan focal objet de la lentille
son plan focal image confondu avec le plan focal objet de la lentille 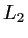 . On note
. On note 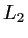 le plan focal image de la seconde lentille.
le plan focal image de la seconde lentille.
![\includegraphics[width=12cm]{abbe_f1f2.eps}](img37.gif)
Dans le plan 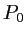 on place une fente de largeur
on place une fente de largeur 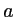 dans la direction
dans la direction  et infinie dans la direction
et infinie dans la direction 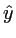 . Elle est éclairée sous incidence normale par une onde plane monochromatique de longueur d'onde
. Elle est éclairée sous incidence normale par une onde plane monochromatique de longueur d'onde 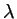 et d'amplitude
et d'amplitude 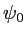 dans le plan
dans le plan 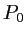 .
.
Dans le plan 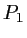 on place un masque de coefficient de transmission
on place un masque de coefficient de transmission
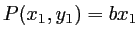 ,
, 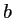 est une constante réelle positive. On rappelle à toutes fins utiles que la transformée de Fourier de
est une constante réelle positive. On rappelle à toutes fins utiles que la transformée de Fourier de 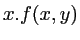 est
est
 (on peut faire le problème sans se servir de cette formule).
(on peut faire le problème sans se servir de cette formule).
- Ecrire l'amplitude complexe
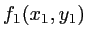 dans le plan
dans le plan 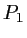 juste après le filtrage par
juste après le filtrage par
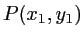 .
.
- Faire le graphe de l'intensité correspondante
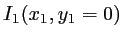 en fonction de
en fonction de 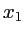 .
.
- Ecrire l'amplitude complexe
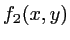 dans le plan
dans le plan 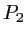 .
.
- Faire le graphe de l'intensité correspondante
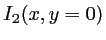 en fonction de
en fonction de 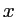 .
.
On complète maintenant le montage précédent par une troisième lentille convergente identique à 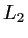 (donc de focale
(donc de focale  ). Le plan
). Le plan 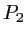 est le plan focal objet de la 3e lentille, on note
est le plan focal objet de la 3e lentille, on note 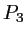 son plan focal image.
son plan focal image.
![\includegraphics[width=17cm]{abbe_triple.eps}](img44.gif)
Dans le plan 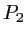 on effectue un second filtrage en plaçant une lame qui multiplie par -1 (déphasage de
on effectue un second filtrage en plaçant une lame qui multiplie par -1 (déphasage de 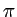 ) l'amplitude complexe
) l'amplitude complexe 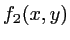 pour
pour 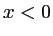 .
.
- Ecrire l'amplitude complexe
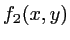 dans le plan
dans le plan 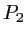 à la sortie de la lame.
à la sortie de la lame.
- En déduire l'amplitude complexe
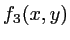 dans le plan
dans le plan 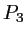 .
.
- Faire le graphe de l'intensité correspondante
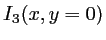 en fonction de
en fonction de 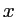 .
.
- Donner le contraste et les frquences spatiales de l'intensité
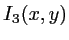
Voir la solution


![\includegraphics[width=12cm]{abbe_f1f2.eps}](img37.gif)
![]() on place une fente de largeur
on place une fente de largeur ![]() dans la direction
dans la direction ![]() et infinie dans la direction
et infinie dans la direction ![]() . Elle est éclairée sous incidence normale par une onde plane monochromatique de longueur d'onde
. Elle est éclairée sous incidence normale par une onde plane monochromatique de longueur d'onde ![]() et d'amplitude
et d'amplitude ![]() dans le plan
dans le plan ![]() .
.
![]() on place un masque de coefficient de transmission
on place un masque de coefficient de transmission
![]() ,
, ![]() est une constante réelle positive. On rappelle à toutes fins utiles que la transformée de Fourier de
est une constante réelle positive. On rappelle à toutes fins utiles que la transformée de Fourier de ![]() est
est
 (on peut faire le problème sans se servir de cette formule).
(on peut faire le problème sans se servir de cette formule).
![\includegraphics[width=17cm]{abbe_triple.eps}](img44.gif)
![]() on effectue un second filtrage en plaçant une lame qui multiplie par -1 (déphasage de
on effectue un second filtrage en plaçant une lame qui multiplie par -1 (déphasage de ![]() ) l'amplitude complexe
) l'amplitude complexe ![]() pour
pour ![]() .
.